Một con lắc lò xo treo thẳng đứng vào điểm I có định, quả cầu có khối lượng 100 g. Con lắc dao động điều hoà theo phương trình: \(x = 4\cos 10\sqrt 5 t(cm)\)với t tính theo giây. Lấy g = 10 \(m/{s^2}\). Tính lực đàn hồi cực đại và cực tiều do lò xo tác dụng lên điểm I.
Tần số góc của con lắc lò xo : \(\)\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{g}{{\Delta l}}} \)
Lực đàn hồi của lò xo : \({F_{dh}} = k\Delta l\)
Tần số góc của con lắc lò xo là :
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{g}{{\Delta l}}} = > 10\sqrt 5 = \sqrt {\frac{k}{{0,1}}} = \sqrt {\frac{{10}}{{\Delta l}}} \)
\( = > \{ _{\Delta l = 0,02(m)}^{k = 50(N/m)}\)
Biên độ dao động của con lắc : \(A = 4cm > \Delta l\) => Vật có thể giãn có thể nén trong quá trình dao động
=> Lực đàn hồi dãn max khi vật ở vị trí thấp nhất :
\({F_{dh\max }} = k.(\Delta l + A) = 50.(0,02 + 0,04) = 3(N)\)
=> Lực đàn hồi nén max khi vật ở vị trí cao nhất :
\({F_{dh\max }} = k.(A - \Delta l) = 50.(0,04 - 0,02) = 1(N)\)
=> Lực đàn hồi min khi vật ở vị trí cân bằng => \({F_{dh\min }} = 0\)

Các bài tập cùng chuyên đề
Ở lớp 10, khi học về chuyển động của vật, ta đã biết có sự chuyển hoá giữa động năng và thế năng của vật. Vậy trong dao động điều hoà có sự chuyển hoá tương tự không?
1. Hình 5.3 là đồ thị động năng và thế năng của một vật dao động điều hòa li độ. Hãy phân tích sự chuyển hóa giữa động năng và thế năng bằng đồ thị

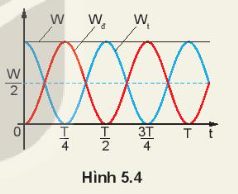
2. Hình 5.4 là đồ thị động năng và thế năng của một vật dao động điều hòa theo thời gian.
a) Động năng và thế năng của vật thay đổi như thế nào trong các khoảng thời gian: từ 0 đến \(\frac{T}{4}\), từ \(\frac{T}{4}\)đến \(\frac{T}{2}\), từ \(\frac{T}{2}\)đến \(\frac{{3T}}{4}\), từ \(\frac{{3T}}{4}\)đến T.
b) Tại các thời điểm: t = 0; t = \(\frac{T}{8}\); t =\(\frac{T}{4}\); t = \(\frac{{3T}}{8}\), động năng và thế năng của vật có giá trị như thế nào (tính theo W). Nghiệm lại để thấy ở mỗi thời điểm đó Wđ + Wt = W.
1. Hình 5.3 là đồ thị động năng và thế năng của một vật dao động điều hòa li độ. Hãy phân tích sự chuyển hóa giữa động năng và thế năng bằng đồ thị

2. Hình 5.4 là đồ thị động năng và thế năng của một vật dao động điều hòa theo thời gian.
a) Động năng và thế năng của vật thay đổi như thế nào trong các khoảng thời gian: từ 0 đến \(\frac{T}{4}\), từ \(\frac{T}{4}\)đến \(\frac{T}{2}\), từ \(\frac{T}{2}\)đến \(\frac{{3T}}{4}\), từ \(\frac{{3T}}{4}\)đến T.
b) Tại các thời điểm: t = 0; t = \(\frac{T}{8}\); t =\(\frac{T}{4}\); t = \(\frac{{3T}}{8}\), động năng và thế năng của vật có giá trị như thế nào (tính theo W). Nghiệm lại để thấy ở mỗi thời điểm đó Wđ + Wt = W.

Chứng minh rằng cơ năng dao động của con lắc đơn tỉ lệ thuận với bình phương của biên độ dao động
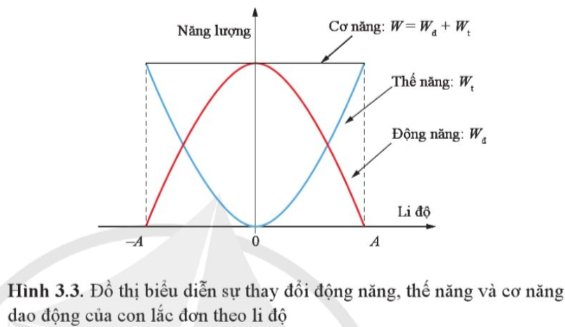
Dựa vào đồ thị Hình 3.3, mô tả sự thay đổi của động năng và thế năng của con lắc đơn khi vật đi từ vị trí biên về vị trí cân bằng và từ vị trí cân bằng đến vị trí biên
Dựa vào đồ thị Hình 3.4, tìm số lần vật có động năng bằng thế năng trong mỗi chu kì dao động của vật
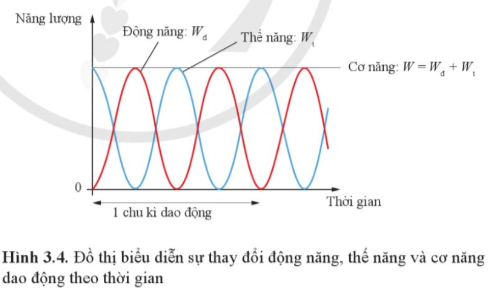
So sánh chu kì biến đổi của động năng và thế năng với chu kì dao động của vật
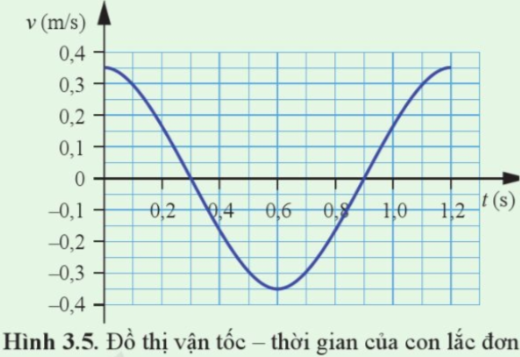
Cho đồ thị vận tốc – thời gian của một con lắc đơn dao động như Hình 3.5. Biết rằng khối lượng của vật treo vào sợi dây là 0,2 kg. Xác định:
a. Chu kì và tần số góc của con lắc.
b. Vận tốc cực đại của con lắc.
c. Cơ năng của con lắc.
d. Biên độ của vật
Khi nghiên cứu sự biến đổi năng lượng của con lắc đơn trong quá trình dao động, có bạn học sinh khẳng định rằng, nếu ta thay một quả lắc khác có khối lượng lớn hơn nhưng vẫn giữ nguyên biên độ của dao động thì vận tốc của quả lắc mới sẽ lớn hơn khi qua vị trí cân bằng vì nó có cơ năng lớn hơn.
Nhận thức này đúng hay sai? Vì sao?
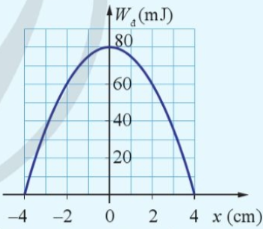
Đồ thị Hình 3.6 mô tả sự thay đổi động năng theo li dộ của quả cầu có khối lượng 0,4 kg trong một con lắc lò xo treo thẳng đứng. Xác định:
a) Cơ năng của con lắc lò xo.
b) Vận tốc cực đại của quả cầu.
c) Thế năng của con lắc lò xo khi quả cầu ở vị trí có li độ 2 cm.
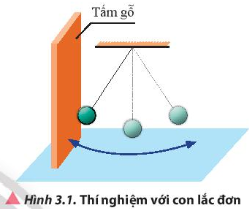
Tiến hành thí nghiệm như mô tả trong Hình 3.1. Đặt một tấm gỗ cố định lên tường, đưa vật nặng của con lắc đơn đến vị trí tiếp xúc với tấm gỗ và thả nhẹ để vật nặng bắt đầu chuyển động không vận tốc ban đầu. Khi dao động, vật nặng có và chạm vào tấm gỗ hay không? Vì sao? Trong quá trình dao động, vật nặng có những dạng năng lượng gì và sự chuyển hoá giữa chúng như thế nào?
Quan sát Hình 3.5 và mô tả sự thay đổi của động năng và thế năng khi vật dao động di chuyển từ biên âm đến biên dương.
1. Quan sát Hình 3.5 và 3.6, nhận xét về độ lớn của động năng, thế năng và cơ năng trong quá trình dao động điều hòa của vật.
2. Dựa vào biểu thức (3.2) và (3.5), hãy thiết lập biểu thức (3.7).
Xét một vật bắt đầu dao động điều hoà từ vị trí cân bằng, hãy chỉ ra những khoảng thời gian trong một chu kì dao động mà:
a) thế năng tăng dần trong khi động năng giảm dần.
b) thế năng giảm dần trong khi động năng tăng dần.
Biết phương trình li độ của một vật có khối lượng 0,2 kg dao động điều hoà là x=5cos(20t) (cm).
a) Tính cơ năng trong quá trình dao động.
b) Viết biểu thức thế năng và động năng.
Một hệ dao động điều hoà với chu kì 2 s. Chọn gốc thế năng tại vị trí cân bằng của vật. Thời điểm hệ bắt đầu dao động thì động năng và thế năng bằng nhau lần thứ nhất. Hỏi sau bao lâu kể từ khi hệ bắt đầu dao động, động năng và thế năng bằng nhau lần thứ hai?
Xét một vật bắt đầu dao động điều hoà từ vị trí cân bằng theo chiều âm của trục toạ độ. Chọn gốc thế năng tại vị trí cân bằng của vật. Hãy vẽ phác đồ thị thể hiện sự phụ thuộc vào thời gian của động năng và thế năng trong hai chu kì dao động trên cùng một hệ trục toạ độ. Chỉ ra trên đồ thị những thời điểm mà động năng và thế năng có độ lớn bằng nhau.
Khi nói về một vật dao động điều hòa với biên độ A và tần số f trong những phát biểu dưới đây.
(1) Cơ năng biến thiên tuần hoàn với tần số 2f
(2) Cơ năng bằng thế năng tại thời điểm vật ở biên.
(3) Cơ năng tỉ lệ thuận với biên độ dao động
(4) Khi vật đi từ vị trí cân bằng ra biên, thể năng giảm, động năng tăng.
(5) Khi vật đi từ biên về vị trí cân bằng thế năng giảm, động năng tăng.
Số phát biểu đúng là
A. 1.
B. 3.
C. 2.
D. 4.
Tỉ số thế năng và cơ năng của một vật dao động điều hòa tại thời điểm tốc độ của vật bằng 25% tốc độ cực đại là bao nhiêu?
A. \(\frac{{15}}{{16}}\)
B. \(\frac{1}{{16}}\)
C. \(\frac{1}{4}\)
D. \(\frac{3}{4}\)
Cho một vật dao động điều hòa thực hiện 20 dao động trong 10 giây, khi vật qua vị trí cân bằng, tốc độ của vật là cm/s. Chọn gốc thời gian là lúc vật ở vị trí có li độ 2 cm và đang chuyển động về vị trí cân bằng. Trong quá trình dao động, thể năng bằng ba lần động năng lần thứ hai kể từ khi bắt đầu chuyển động tại thời điểm nào?
A. \(t = \frac{1}{{24}}s\)
B. \(t = \frac{1}{8}s\)
C. \(t = \frac{5}{{24}}s\)
D. \(t = \frac{7}{{24}}s\)
Cho khối lượng của vật dao động là 300 g và phương trình li độ của một vật dao động điều hoà là \(x = 10\cos \left( {20t + \frac{\pi }{3}} \right)\) cm. Tính cơ năng trong quá trình dao động.
Một vật khối lượng 2 kg có thể dao động điều hoà trên mặt phẳng nằm ngang không ma sát với tần số góc là 4 rad/s. Để kích thích vật dao động điều hòa, tại thời điểm t = 0, kéo vật ra khỏi vị trí cân bằng 10 cm và truyền cho vật một vận tốc có độ lớn 1 m/s hướng về vị trí cân bằng. Hãy xác định
a) Động năng của vật tại vị trí cân bằng.
b) Biên độ dao động của vật
c) Tỉ số động năng và thế năng tại vị trí x = 15 cm.
d) Tốc độ của vật tại vị trí mà động năng bằng 5/11 thể năng.
Đại lượng nào sau đây tăng gấp đôi khi tăng gấp đôi biên độ của dao động điều hoà của con lắc lò xo?
A. Cơ năng của con lắc.
B. Động năng của con lắc.
C. Vận tốc cực đại.
D. Thế năng của con lắc.
Cơ năng của một chất điểm dao động điều hoà tỉ lệ thuận với
A. chu kì dao động.
B. biên độ dao động.
C. bình phương biên độ dao động.
D. bình phương chu kì dao động.
Trong dao động điều hoà thì tập hợp 3 đại lượng nào sau đây không thay đồi theo thời gian?
A. Lực kéo về ; vận tốc ; năng lượng toàn phần.
B. Biên độ ; tần số góc ; gia tốc.
C. Động năng ; tần số ; lực kéo về.
D. Biên độ , tần số góc ; năng lượng toàn phần.
Một vật có khối lượng m = 1 kg, dao động điều hoà với chu kì \(T = 0,2\pi \left( s \right)\), biên độ dao động bằng 2 cm. Tính cơ năng của dao động.
Một con lắc lò xo treo thẳng đứng. Biết rằng trong quá trình dao động tỉ số giữa lực đàn hồi cực đại và cực tiểu là \(\frac{7}{3}\) , biên độ dao động là 10 cm. Lấy g = 10 \(m/{s^2}\) . Tính tần số dao động của vật.
Một con lắc lò xo gồm một lò xo nhẹ có độ cứng k và một vật có khối lượng m = 100 g, được treo thằng đứng vào một giá cố định. Tại vị trí cân bằng O của vật, lò xo giãn 2,5 cm. Kéo vật dọc theo trục của lò xo xuống dưới cách vị trí cân bằng O một đoạn 2 cm rồi truyền cho nó vận tốc \(40\sqrt 3 \)cm/s theo phương thẳng đứng hướng xuống dưới. Chọn trục tọa độ Ox theo phương thẳng đứng, góc tại O, chiều dương hướng lên trên, gốc thời gian là lúc vật bắt đầu dao động. Lấy g = 10 \(m/{s^2}\). Biết chiều dài tự nhiên của của lò
xo là 50 cm.
a) Tính độ cứng của lò xo, viết phương trình dao động và tính cơ năng
của vật.
b) Xác định li độ và vận tốc của vật khi thế năng bằng \(\frac{1}{3}\) động năng.
c) Tính thế năng, động năng và vận tốc của vật tại vị trí có li độ x= 2 cm.
d) Tính chiều dài, lực đàn hồi cực đại, cực tiều của lò xo trong quá trình
dao động.
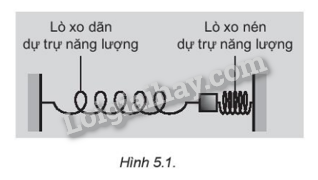
Hãy phân tích sự chuyển hoá năng lượng giữa động năng và thế năng trong hệ gồm hai lò xo và vật nặng m được mắc như Hình 5.1. Khi quả nặng được thả cho dao động.
Một người khối lượng 83 kg treo mình vào sợi dây bungee đàn hồi
có độ cứng k= 270 N/m (Hình 5.2). Từ vị trí cân bằng người này được kéo đến vị trí mà sợi dây dãn thêm 5 m so với chiều dài tự nhiên và dao động điều hoà. Xác định vị trí và vận tốc của người này sau 2 s.








Danh sách bình luận