Tìm đa thức V sao cho
\(V + 4{y^3} - 2x{y^2} + {x^2}y - 9 = 4{y^3} - 3\)
Chuyển vế, tìm V.
Ta xét
\(V + 4{y^3} - 2x{y^2} + {x^2}y - 9 = 4{y^3} - 3\)
\( V = 4{y^3} - 3 - 4{y^3} + 2x{y^2} - {x^2}y + 9\)
\( V = \left( {4{y^3} - 4{y^3}} \right) + \left( { - 3 + 9} \right) + 2x{y^2} - {x^2}y\)
\( V = 6 + 2x{y^2} - {x^2}y\).
Vậy \(V = 6 + 2x{y^2} - {x^2}y\).

Các bài tập cùng chuyên đề
Thực hiện phép trừ hai đa thức A và B bằng cách lập hiệu
\(A - B = \left( {5{x^2}y + 5x - 3} \right) - \left( {xy - 4{x^2}y + 5x - 1} \right)\), bỏ dấu ngoặc rồi thu gọn đa thức nhận được.
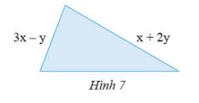
Tìm độ dài cạnh còn thiếu của tam giác ở Hình 7, biết rằng tam giác có chu vi bằng \(7x + 5y\).
Cho hai đa thức: \(P = {x^2} + 2{\rm{x}}y + {y^2}\) và \(Q = {x^2} - 2{\rm{x}}y + {y^2}\)
a) Viết hiệu P – Q theo hàng ngang, trong đó đa thức Q được đặt trong dấu ngoặc
b) Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức Q, nhóm các đơn thức đồng dạng với nhau.
c) Tính hiệu P – Q bằng cách thực hiện phép tính trong từng nhóm .
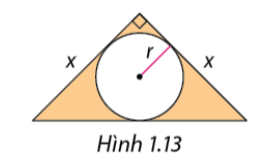
Viết một đa thức biểu diễn diện tích của phần được tô màu trong Hình 1.13.
Cho A và B là hai đa thức. Biết rằng \(A = 4{x^3}{y^2} - 2{x^2}{y^3} + x{y^2} - 2,5\) và \(A + B = 3{x^2}{y^3} + 0,5\) .
Khi đó ta có
A. \(B = - 4{x^3}{y^2} + 5{x^2}{y^3} - x{y^2} + 3\) .
B. \(B = 4{x^3}{y^2} + {x^2}{y^3} + x{y^2} - 2\) .
C. \(B = - 4{x^3}{y^2} + {x^2}{y^3} - x{y^2} + 2\) .
D. \(B = 4{x^3}{y^2} - 5{x^2}{y^3} + x{y^2} - 3\) .
Tìm đa thức M biết \(M - 5{x^2} + xyz = xy + 2{x^2} - 3xyz + 5\)
Biết \(M + 5{x^2} - 2xy = 6{x^2} + 10xy - {y^2}\). Đa thức \(M\) là
-
A.
\(M = {x^2} + 12xy - {y^2}\).
-
B.
\(M = {x^2} - 12xy - {y^2}\).
-
C.
\(M = {x^2} - 12xy + {y^2}\).
-
D.
\(M = - {x^2} - 12xy + {y^2}\).
Cho
\(\begin{array}{l}M = x - (y - z) - 2{{x}} + y + z - (2 - x - y)\\N = x - \left[ {x - \left( {y - 2{{z}}} \right) - 2{{z}}} \right]\end{array}\)
Tính M – N
-
A.
-2z + 2
-
B.
-2x – 2y – 2
-
C.
2z – 2
-
D.
-2x + 2y - 2







Bình luận