Cho \(\alpha \) là góc vuông. Chứng minh \(\frac{a}{{\sin \alpha }} = 2R.\)
Bước 1: Xác định đường tròn ngoài tiếp tam giác, từ đó suy ra bán kính R
Bước 2: Tính \(\frac{a}{{\sin \alpha }}\) rồi so sánh với 2R.
Xét tam giác ABC có \(\widehat A = \alpha = {90^o}\)
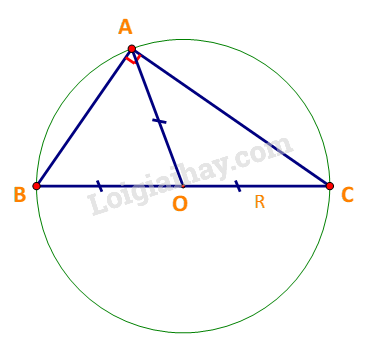
Gọi O là trung điểm của BC. Khi đó: \(OA = OB = OC = \frac{1}{2}BC\)
Do đó đường tròn ngoại tiếp tam giác ABC là (O) bán kính \(R = \frac{{BC}}{2}\)
\( \Rightarrow \frac{a}{{\sin \alpha }} = \frac{{BC}}{{\sin {{90}^o}}} = BC = 2R\) (đpcm)
Các bài tập cùng chuyên đề
Cho tam giác ABC có b = 8, c = 5 và \(\widehat B = {80^o}\). Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài cạnh còn lại của tam giác.
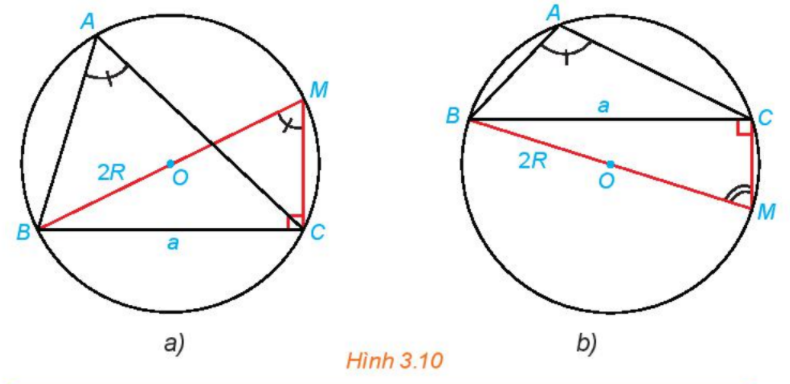
Trong mỗi hình dưới dây, hãy tính R theo a và sinA.
Cho tam giác ABC có \(a = 10,\widehat A = {45^o},\widehat B = {70^o}\). Tính R,b,c.
b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.
b) Tính chiều cao của tòa nhà.
A. \(R = \frac{a}{{\sin A}}\)
B. \(R = \frac{{\sqrt 2 }}{2}b\)
C. \(R = \frac{{\sqrt 2 }}{2}c\)
D. \(R = \frac{{\sqrt 2 }}{2}a\)
Cho tam giác ABC nội tiếp đường tròn (O) có bán kính R = 6 và có các góc \(\widehat B = {65^o},\widehat C = {85^o}.\) Tính độ dài cạnh BC.
Cho tam giác ABC có \(\widehat B = {75^o},\widehat C = {45^o}\) và BC = 50. Tính độ dài cạnh AB.
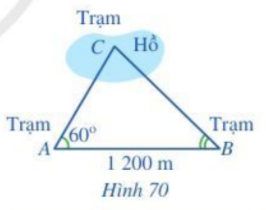
Có hai trạm quan sát A và B ven hồ và một trạm quan sát C ở giữa hồ. Để tính khoảng cách từ A và B đến C, người ta làm như sau:
- Đo góc BAC được \({60^o}\), đo góc ABC được \({45^o}\);
- Đo khoảng cách AB được 1 200 m.
Khoảng cách từ trạm C đến các trạm A và B bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
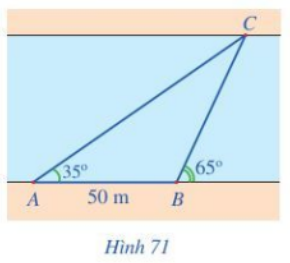
Một người đứng ở bờ sông, muốn đo độ rộng của khúc sông chảy qua vị trí đang đứng (khúc sông tương đối thẳng, có thể xem hai bờ sông song song với nhau.)
Từ vị trí đang đứng A, người đó đo được góc nghiêng \(\alpha = {35^o}\)so với bờ sông tới một vị trí C quan sát được ở phía bờ bên kia. Sau đó di chuyển dọc bờ sông đến vị trí B cách A một khoảng d = 50 m và tiết tục đo được góc nghiêng \(\beta = {65^o}\) so với bờ bên kia tới vị trí C đã chọn (Hình 71). Hỏi độ rộng của khúc sông chảy qua vị trí người đó đang đứng là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
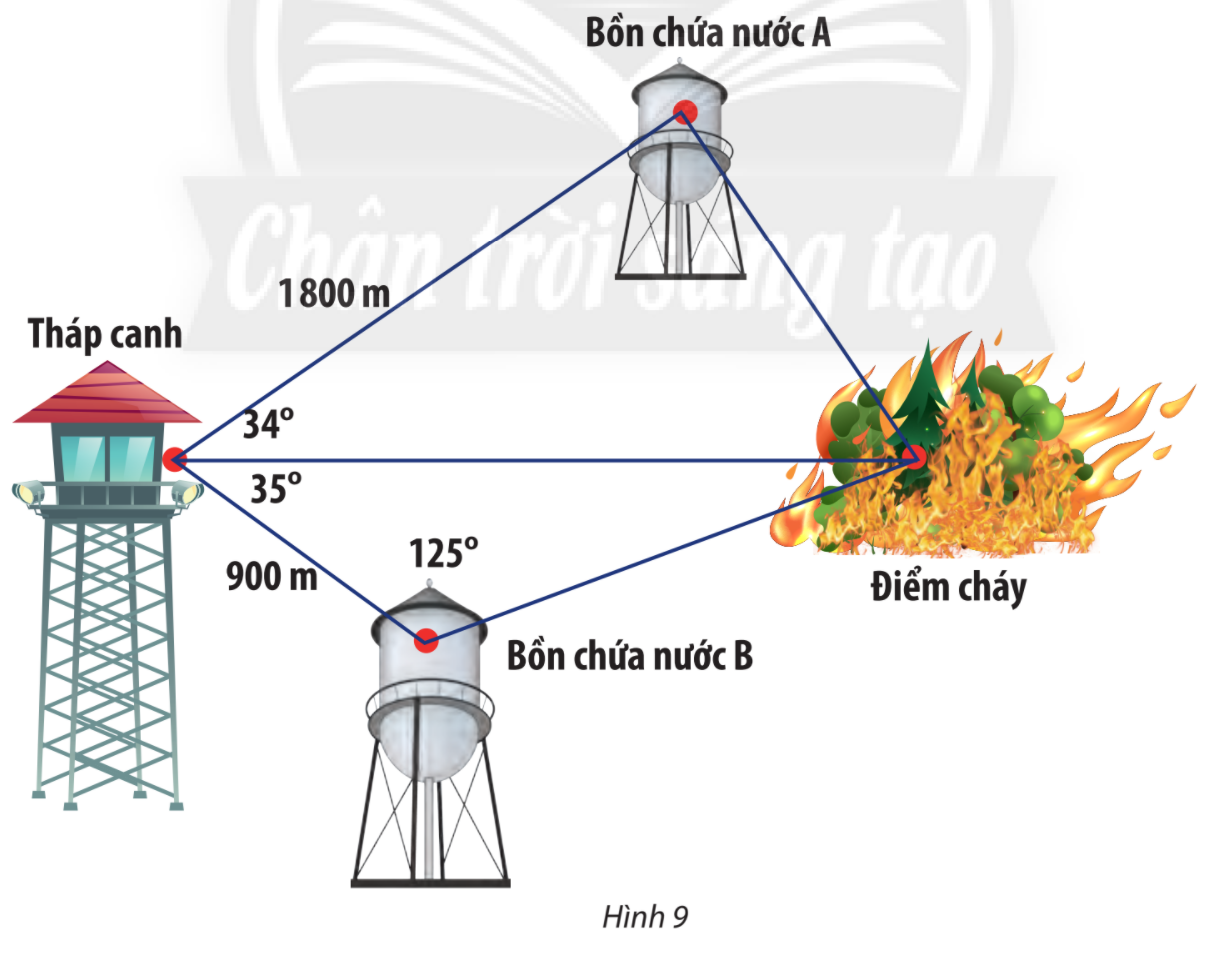
Trong một khu bảo tồn, người ta xây dựng một tháp canh và hai bồn chứa nước A, B để phòng hỏa hoạn. Từ tháp canh, người ta phát hiện đám cháy và số liệu đưa về như Hình 9. Nên dẫn nước từ bồn chứa A hay B để dập tắt đám cháy nhanh hơn?
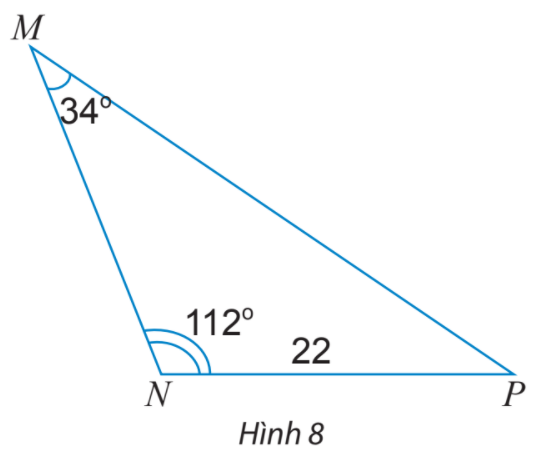
Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình 8.
a) Cho tam giác ABC không phải là tam giác vuông có \(BC = a,AC = b,AB = c\) và R là bán kính của đường trong ngoại tiếp tam giác đó. Vẽ đường kính BD.
i) Tính \(\sin \widehat {BDC}\) theo a và R.
ii) Tìm mối liên hệ giữa hai góc \(\widehat {BAC}\) và \(\widehat {BDC}\). Từ đó chứng minh rằng \(2R = \frac{a}{{\sin A}}.\)
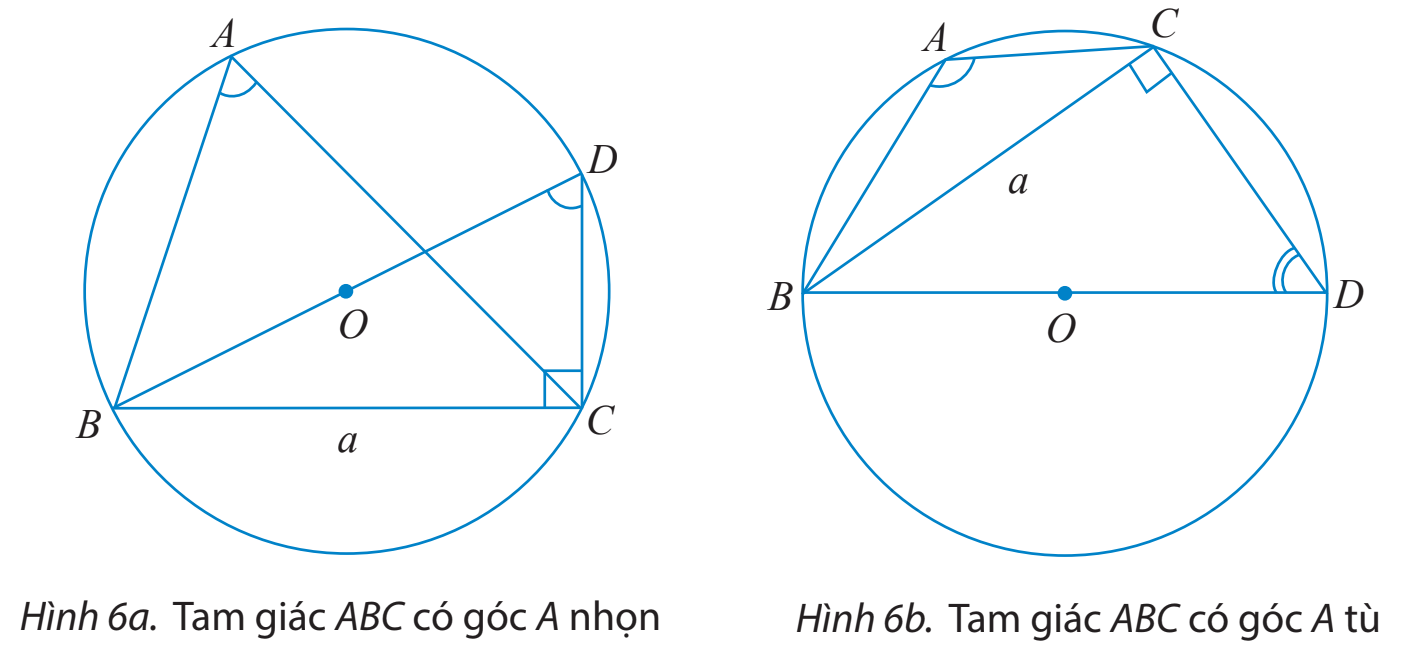
b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức \(2R = \frac{a}{{\sin A}}.\)
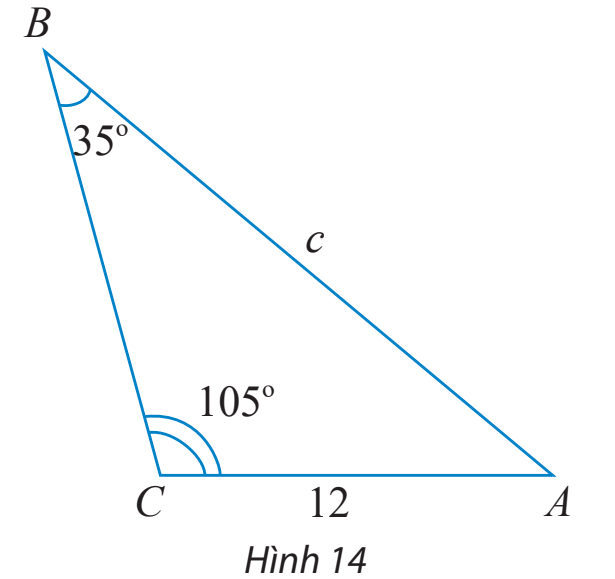
Tính độ dài cạnh c trong tam giác ABC ở Hình 14.
Cho tam giác ABC, biết cạnh \(a = 152,\;\widehat B = {79^o},\;\widehat C = {61^o}.\) Tính các góc, các cạnh còn lại và bán kính đường tròn ngoại tiếp của tam giác đó.
Cho \({h_a}\) là đường cao vẽ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh hệ thức: \({h_a} = 2R\sin B\sin C.\)
Trong tam giác ABC với BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp tam giác ABC. Hệ thức nào sau đây đúng?
Tam giác \(ABC\) có \(\widehat A = {45^ \circ },\,\,c = 6,\,\,\widehat B = {75^ \circ }.\) Độ dài bán kính đường tròn ngoại tiếp của tam giác bằng:
A. \(8\sqrt 3 .\)
B. \(2\sqrt 3 .\)
C. \(6\sqrt 3 .\)
D. \(4\sqrt 3 .\)
Cho tam giác ABC có \(AB = 8\) cm, \(AC = 18\) cm và có diện tích bằng 64 cm2. Giá trị \(\sin A\) là:
A. \(\frac{{\sqrt 3 }}{2}\)
B. \(\frac{3}{8}\)
C. \(\frac{4}{5}\)
D. \(\frac{8}{9}\)
Cho \(\widehat {xOy} = 30^\circ \). Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho \(AB = 1\). Độ dài lớn nhất của đoạn OB bằng:
A. 1,5
B. \(\sqrt 3 \)
C. \(2\sqrt 2 \)
D. 2
Cho tam giác ABC có \(\widehat B = {60^0},\widehat C = {105^0}\) và \(BC = 15\). Tính độ dài cạnh AC và bán kính R của đường tròn ngoại tiếp tam giác ABC (làm tròn kết quả đến hàng phần mười).
Từ một tấm tôn hình tròn bán kính R = 1 m, bạn trí muốn cắt ra một hình tam giác ABC có các góc A = 450, B = 750. Hỏi bạn Trí phải cắt miếng tôn theo hai dây cung AB, BC có độ dài lần lượt bằng bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Một cây cao bị nghiêng so với mặt đất góc 780. Từ vị trí C cách gốc cây 20 m, người ta tiến hành đo đạc và thu được kết quả \(\widehat {ACB} = {50^0}\) với B là vị trí ngọn cây (Hình 10). Tính khoảng cách từ gốc cây (điểm A) đến ngọn cây (điểm B) (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
Cho tam giác ABC có \(BC = 50\)cm, \(\widehat B = {65^0},\widehat C = {45^0}\). Tính (làm tròn kết quả đến hàng phần mười theo đơn vị xentimet).
a) Độ dài cạnh AB, AC.
b) Bán kính đường tròn ngoại tiếp tam giác ABC.
Cho tam giác ABC có AB = c, AC = b, CB = a, R là bán kính đường tròn ngoại tiếp. Hệ thức nào sau đây là sai?
