Cho đường thẳng mn cắt đường thẳng xy và uv lần lượt tại hai điểm P và Q (H.3.17).Em hãy kể tên:
a) Hai cặp góc so le trong
b) Bốn cặp góc đồng vị.
Vẽ hình, nhận diện các cặp góc so le trong, đồng vị.
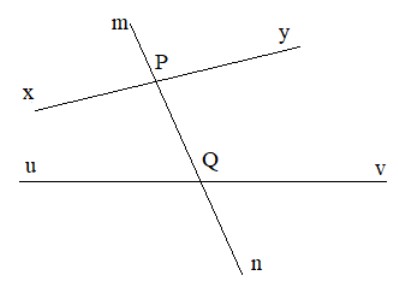
a) Hai cặp góc so le trong là: góc xPn và góc mQv; góc yPn và góc uQm
b) Bốn cặp góc đồng vị là: góc mPy và góc mQv; góc yPn và góc vQn; góc mPx và góc mQu; góc xPn và góc uQn.

Các bài tập cùng chuyên đề
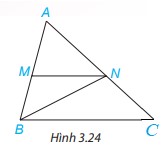
Quan sát hình 3.24.
a) Tìm một góc ở vị trí so le trong với góc MNB.
b) Tìm một góc ở vị trí đồng vị với góc ACB.
c) Kể tên một cặp góc trong cùng phía.
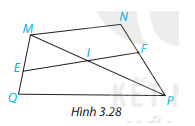
Cho Hình 3.28.
a) Tìm các góc ở vị trí so le trong với góc FIP; NMI
b) Tìm các góc ở vị trí đồng vị với góc EQP; IFP.
Quan sát hình 3.5.
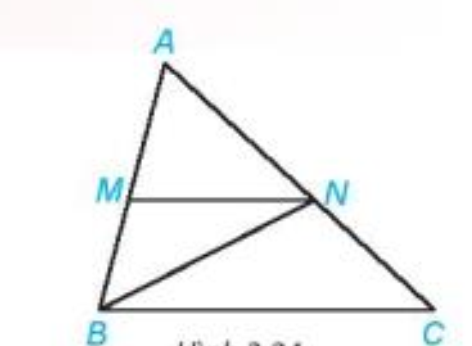
a) Tìm một góc ở vị trí so le trong với góc MNB.
b) Tìm một góc ở vị trí đồng vị với góc ACB.
c) Kể tên một cặp góc trong cùng phía.
d) Biết MN // BC, em hãy kể tên ba cặp góc bằng nhau trong hình vẽ.
Cho hình vẽ bên, \(\widehat {BAH}\) và \(\widehat {CBE}\) là một cặp góc
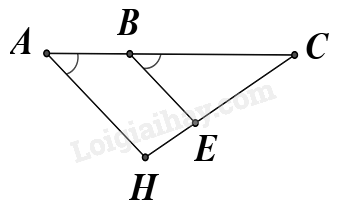
-
A.
bù nhau.
-
B.
trong cùng phía.
-
C.
so le trong.
-
D.
đồng vị.
Chọn phát biểu đúng.
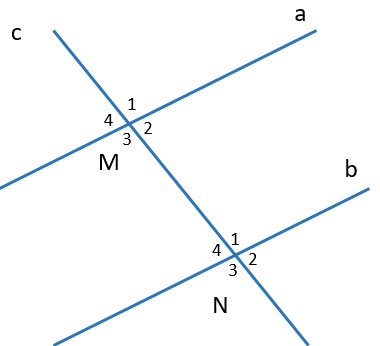
-
A.
\(\widehat {{M_1}}\) và \(\widehat {{N_1}}\) là hai góc so le trong;
-
B.
\(\widehat {{M_2}}\) và \(\widehat {{N_2}}\) là hai góc so le ngoài
-
C.
\(\widehat {{M_3}}\) và \(\widehat {{N_1}}\) là hai góc đồng vị
-
D.
\(\widehat {{M_4}}\) và \(\widehat {{N_4}}\) là hai góc đồng vị
Chọn một cặp góc đồng vị trong hình vẽ sau:
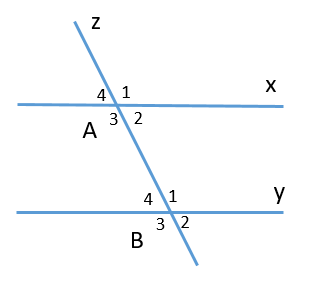
-
A.
\(\widehat {{B_2}}\) và \(\widehat {{B_3}}\);
-
B.
\(\widehat {{A_3}}\) và \(\widehat {{B_3}}\);
-
C.
\(\widehat {{A_2}}\) và \(\widehat {{B_4}}\);
-
D.
\(\widehat {{A_4}}\) và \(\widehat {{A_2}}\).
Chọn hình vẽ. Em hãy chọn câu trả lời đúng.
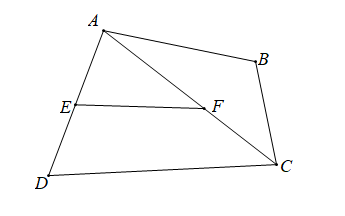
-
A.
\(\widehat {DAC}\) và \(\widehat {AFE}\) là hai góc so le trong;
-
B.
\(\widehat {AFE}\) và \(\widehat {BAC}\) là hai góc so le trong;
-
C.
\(\widehat {AFE}\) và \(\widehat {ADC}\) là hai góc đồng vị;
-
D.
\(\widehat {BAC}\) và \(\widehat {DAC}\) là hai góc đồng vị.
Chọn hình vẽ. Em hãy chọn câu trả lời đúng.
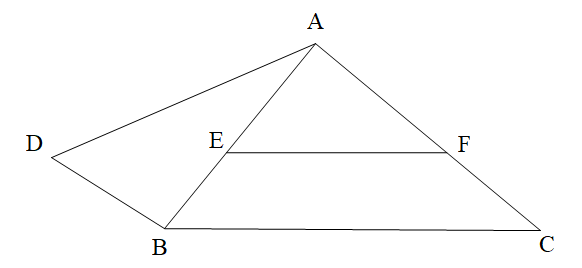
-
A.
\(\widehat {DAB}\) và \(\widehat {EAD}\) là hai góc so le trong;
-
B.
\(\widehat {AFE}\) và \(\widehat {BAC}\) là hai góc so le trong;
-
C.
\(\widehat {AFE}\) và \(\widehat {ACB}\) là hai góc đồng vị;
-
D.
\(\widehat {BAC}\) và \(\widehat {DAB}\) là hai góc đồng vị.