Em hãy nhắc lại thứ tự thực hiện phép tính đối với số tự nhiên rồi tính:

\(\begin{array}{l}a)10 + 36:2.3;\\b)[5 + 2.(9 - {2^3})]:7\end{array}\)

Tính giá trị của các biểu thức sau:

\(\begin{array}{l}a)\left( {\frac{2}{3} + \frac{1}{6}} \right):\frac{5}{4} + \left( {\frac{1}{4} + \frac{3}{8}} \right):\frac{5}{2}\\b)\frac{5}{9}:\left( {\frac{1}{{11}} - \frac{5}{{22}}} \right) + \frac{7}{4}.\left( {\frac{1}{{14}} - \frac{2}{7}} \right)\end{array}\)

Tính một cách hợp lí

\(\begin{array}{l}a) - 1,2 + ( - 0,8) + 0,25 + 5,75 - 2021\\b) - 0,1 + \frac{{16}}{9} + 11,1 + \frac{{ - 20}}{9}\end{array}\)

Để làm một cái bánh, cần \(2\frac{3}{4}\) cốc bột. Lan đã có \(1\frac{1}{2}\) cốc bột. Hỏi Lan cần thêm bao nhiêu cốc bột nữa?

Tính một cách hợp lí:

\(\begin{array}{l}a)A = 32,125 - (6,325 + 12,125) - (37 + 13,675)\\b)B = 4,75 + {\left( {\frac{{ - 1}}{2}} \right)^3} + 0,{5^2} - 3.\frac{{ - 3}}{8}\\c)C = 2021,2345.2020,1234 + 2021,2345.( - 2020,1234)\end{array}\)

Đặt một cặp dấu ngoặc “( )” vào biểu thức sau để được kết quả bằng 0.

2,2 – 3,3 + 4,4 – 5,5.

Tính:

a)\(1\frac{1}{2} + \frac{1}{5}.\left[ {\left( { - 2\frac{5}{6} + \frac{1}{3}} \right)} \right];\)      

b)\(\frac{1}{3}.\left( {\frac{2}{5} - \frac{1}{2}} \right):{\left( {\frac{1}{6} - \frac{1}{5}} \right)^2}.\)

Tính nhanh:

a)\(\frac{{13}}{{23}}.\frac{7}{{11}} + \frac{{10}}{{23}}.\frac{7}{{11}};\)                                          

b) \(\frac{5}{9}.\frac{{23}}{{11}} - \frac{1}{{11}}.\frac{5}{9} + \frac{5}{9}\)

c)\(\left[ {\left( { - \frac{4}{9}} \right) + \frac{3}{5}} \right]:\frac{{13}}{{17}} + \left( {\frac{2}{5} - \frac{5}{9}} \right):\frac{{13}}{{17}};\)                

d) \(\frac{3}{{16}}:\left( {\frac{3}{{22}} - \frac{3}{{11}}} \right) + \frac{3}{{16}}:\left( {\frac{1}{{10}} - \frac{2}{5}} \right)\)

a)      Tính diện tích hình thang ABCD có các kích thước như hình sau:

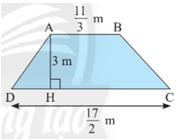
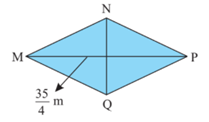
b)      Hình thoi MNPQ có diện tích bằng diện tích hình thang ABCD ở câu a, đường chéo MP= \(\frac{{35}}{4}\)m. Tính độ dài NQ.

Tìm số hữu tỉ a, biết rằng lấy a nhân với \(\frac{1}{2}\) rồi cộng với \(\frac{3}{4}\), sau đó chia kết quả cho \(\frac{{ - 1}}{4}\) thì được số \( - 3\frac{3}{4}\).

Tính giá trị của mỗi biểu thức sau:

a) \(0,2 + 2,5:\frac{7}{2}\)

b) \(9.{\left( {\frac{{ - 1}}{3}} \right)^2} - {\left( { - 0,1} \right)^3}:\frac{2}{{15}}\)

Tính giá trị của mỗi biểu thức sau:

a) \(\left( {0,25 - \frac{5}{6}} \right).1,6 + \frac{{ - 1}}{3}\)

b) \(3 - 2.\left[ {0,5 + \left( {0,25 - \frac{1}{6}} \right)} \right]\)

Tính

a) \(\frac{1}{9} - 0,3.\frac{5}{9} + \frac{1}{3};\)

b) \({\left( {\frac{{ - 2}}{3}} \right)^2} + \frac{1}{6} - {\left( { - 0,5} \right)^3}.\)

Tính

a) \(\left( {\frac{4}{5} - 1} \right):\frac{3}{5} - \frac{2}{3}.0,5\)

b) \(1 - {\left( {\frac{5}{9} - \frac{2}{3}} \right)^2}:\frac{4}{{27}}\)

c)\(\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4\)

d) \(0,8:\left\{ {0,2 - 7.\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} - \frac{5}{{14}}} \right)} \right]} \right\}\)

Một mảnh vườn có dạng hình chữ nhật với độ dài hai cạnh là 5,5 m và 3,75 m. Dọc theo các cạnh của mảnh vườn, người ta trồng các khóm hoa, cứ \(\frac{1}{4}\)m trồng một khóm hoa. Tính số khóm hoa cần trồng.

Cho miếng bìa có kích thước như hình vẽ bên (các số đo trên hình tính theo đơn vị đề-xi-mét).

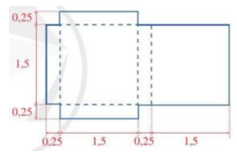
a) Tính diện tích của miếng bìa.

b) Từ miếng bìa đó, người ta gấp thành một hình hộp chữ nhật. Tính thể tích của hình hộp chữ nhật đó.

Tính:

a)\(0,3 - \frac{4}{9}:\frac{4}{3} \cdot \frac{6}{5} + 1\);

b)\({\left( {\frac{{ - 1}}{3}} \right)^2} - \frac{3}{8}:{(0,5)^3} - \frac{5}{2} \cdot ( - 4)\);

c)\(1 + 2:\left( {\frac{2}{3} - \frac{1}{6}} \right) \cdot ( - 2,25)\)

d)\(\left[ {\left( {\frac{1}{4} - 0,5} \right) \cdot 2 + \frac{8}{3}} \right]:2\).

Tính \(A = \left[ {\left( {\dfrac{1}{{81}} - \dfrac{3}{{162}}} \right).\dfrac{{81}}{{17}} + \dfrac{{35}}{{34}}} \right]:\left[ {\left( {\dfrac{9}{{51}} - \dfrac{7}{{102}}} \right).\dfrac{{102}}{5} + 2017} \right]\)

Tính

a)\(\left( { - 0,5} \right) - \left( { - 1 + \dfrac{2}{3}} \right):1,5 + \left( {\dfrac{{ - 1}}{4}} \right)\)

b)\(\left[ {\left( {\dfrac{{ - 7}}{8}} \right):\dfrac{{21}}{{16}}} \right] - \dfrac{5}{3}.\left( {\dfrac{1}{3} - \dfrac{7}{{10}}} \right)\)

c)\({\left[ {\left( {\dfrac{{ - 2}}{3}} \right) + \dfrac{3}{4}} \right]^2}.\dfrac{{12}}{5} - \dfrac{1}{5}\)

d)\({\left( {\dfrac{1}{{25}} - 0,4} \right)^2}:\dfrac{9}{{125}} - \left[ {\left( {1\dfrac{1}{3} - \dfrac{2}{5}} \right).\dfrac{3}{7}} \right]\)

e)\(\left\{ {3\dfrac{{17}}{{18}}.\left[ {\dfrac{5}{2} - \left( {\dfrac{1}{3} + \dfrac{2}{9}} \right)} \right]} \right\}:{\left[ {\left( {\dfrac{{ - 1}}{2}} \right) + 0,25} \right]^2}\) 

Tính giá trị của mỗi biểu thức sau:

a) \(12.{\left( {\dfrac{2}{3} - \dfrac{5}{6}} \right)^2}\);

b) \(4.{\left( { - \dfrac{1}{2}} \right)^3} - 2.{\left( { - \dfrac{1}{2}} \right)^2} + 3.\left( { - \dfrac{1}{2}} \right) + 1\).

Tính giá trị của mỗi biểu thức sau:

a) \(\dfrac{{45}}{4} - \left( {2\dfrac{5}{7} + 5,25} \right)\);

b) \(\dfrac{5}{9}:2,4 - \dfrac{{41}}{9}:2,4\);

c) \(\left( { - \dfrac{3}{4} + \dfrac{5}{{13}}} \right).\dfrac{7}{2} - \left( {\dfrac{9}{4} - \dfrac{8}{{13}}} \right).\dfrac{7}{2}\).

Cho \(A = \dfrac{{13}}{{50}}.( - 15,5) - \dfrac{{13}}{{50}}.84\dfrac{1}{2};{\rm{ }}B = \dfrac{{{{( - 0,7)}^2}.{{( - 5)}^3}}}{{{{\left( { - \dfrac{7}{3}} \right)}^3}.{{\left( {\dfrac{3}{2}} \right)}^4}.{{( - 1)}^5}}}\).

Bạn An tính được giá trị của các biểu thức trên: \(A =  - 26;{\rm{ }}B = \dfrac{{ - 20}}{{21}}\). Theo em, bạn An tính đúng hay sai?

Cho \(A = \dfrac{{\dfrac{{ - 1}}{2} - 5.{{\left( {\dfrac{3}{2}} \right)}^2}}}{{15\dfrac{2}{9} + {{\left( { - \dfrac{2}{3}} \right)}^2}}};{\rm{ }}B = \dfrac{7}{{12}}.3,4 - \dfrac{7}{{12}}.8,8\).

Tính \(A - 5B\).

Chọn dấu “<”, “>”, “=” thích hợp cho :

a) \(\dfrac{5}{6} - {\left( {\dfrac{1}{6}} \right)^2}\) ... \({\left( {\dfrac{5}{6} - \dfrac{1}{6}} \right)^2}\);

b) \(250.{\left( {\dfrac{1}{5} - \dfrac{1}{6}} \right)^2}\) ... \(250.{\left( {\dfrac{1}{5}} \right)^2} - \dfrac{1}{6}\);

c) \(3\dfrac{1}{5}:1,5 + 4\dfrac{2}{5}:1,5\) ... \(\left( {3\dfrac{1}{5} + 4\dfrac{2}{5}} \right):1,5\);

d) \(\left( {\dfrac{9}{{25}} - 2,18} \right):\left( {3\dfrac{4}{5} + 0,2} \right)\) ... \(\dfrac{9}{{25}}:3\dfrac{4}{5} - 2,18:0,2\).

Cho \(A = \left( {17,81:1,37 - \dfrac{{59}}{3}:\dfrac{{11}}{6}} \right) + \dfrac{{{{(0,8)}^3}}}{{{{(0,4)}^3}.11}}\).

Chứng minh rằng A + 1 là bình phương của một số tự nhiên.

Một vườn trường có dạng hình chữ nhật với độ dài hai cạnh là 26 m và 14 m. Người ta muốn rào xung quanh vườn, cứ cách 2 m đóng một cọc rào, mỗi góc vườn đều đóng một cọc rào và chỉ để một cửa ra vào vườn rộng 4 m. Tính số cọc rào cần dùng, biết rằng hai cạnh bên của cửa đồng thời cũng là hai cọc rào.

Quan sát biển báo giao thông ở Hình 7.

a) Tính diện tích của biển báo, biết rằng đường kính của biển báo là 87,5 cm (lấy \(\pi  = 3,14\)).

b) Ở chính giữa của biển báo là hình chữ nhật được sơn màu trắng có chiều dài là 70,3 cm và chiều rộng là 12,3 cm. Phần còn lại của biển báo được sơn màu đỏ. Tính diện tích phần được sơn màu đỏ của biển báo.

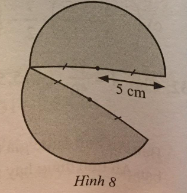
Người ta cắt một tấm tôn có dạng hình tròn bán kính 5 cm thành hai phần bằng nhau như Hình 8. Tính chu vi tấm tôn sau khi bị cắt (lấy \(\pi  = 3,14\)).

Tính một cách hợp lí.

a, \( - 1,2 + \left( { - 0,8} \right) + 0,25 + 5,75 - 2021;\)

b, \( - 0,1 + \frac{{16}}{9} + 11,1 + \frac{{ - 20}}{9}.\)

Để làm một cái bánh, cần \(2\frac{3}{4}\) cốc bột. Lan đã có \(1\frac{1}{2}\) cốc bột. Hỏi Lan cần thêm bao nhiêu cốc bột nữa?

Một ô tô đã đi 110 km trong 3 giờ. Trong giờ thứ nhất, xe đi được \(\frac{1}{3}\) quãng đường. Trong giờ thứ hai, xe đi được \(\frac{2}{5}\) quãng đường còn lại. Hỏi trong giờ thứ ba xe đi được bao nhiêu ki-lô-mét?