Hằng ngày chúng ta thấy rất nhiều chuyển động, trong đó vật chuyển động qua lại quanh một vị trí cân bằng. Chuyển động của người chơi đu là một ví dụ như vậy (Hình 1.1).

Những chuyển động đó được gọi là dao động. Mô tả dao động như thế nào?
Nhớ lại về các chuyển động được gọi là dao động trong cuộc sống thường ngày: dây đàn ghita rung động, màng trống rung động, … Những chuyển động này có điểm chung là gì?
Dao động là chuyển động mà vật chuyển động qua lại quanh một vị trí đặc biệt gọi là vị trí cân bằng.

Các bài tập cùng chuyên đề
Trong cuộc sống hằng ngày và trong kĩ thuật ta thường gặp những vật dao động, ví dụ như dây đàn ghi ta rung động, chiếc đu đung đưa, pít-tông chuyển động lên xuống trong xi lanh của động cơ,... Chuyển động của những vật này được gọi là dao động cơ. Vậy dao động cơ có những đặc điểm gì chung?
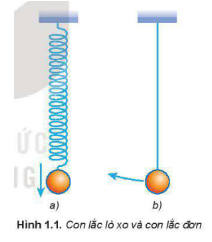
Treo một vật nhỏ, nặng vào đầu tự do của một lò xo nhẹ (Hình 1.1a) hoặc một dây nhẹ không dãn ta có con lắc lò xo hoặc con lắc đơn (Hình 1.1b).
1. Xác định vị trí cân bằng của vật.
2. Kéo vật lệch khỏi vị trí cân bằng rồi thả ra cho chuyển động. Quan sát chuyển động của mỗi vật và cho nhận xét về đặc điểm chung của chúng.
Nêu những ví dụ về dao động cơ mà em biết.
Dùng một lò xo, một quả cầu nhỏ bằng kim loại, sợi dây và giá thí nghiệm, thảo luận với bạn xây dựng phương án và thực hiện phương án tạo ra dao động của quả cầu treo ở một đầu lò xo.
Nêu ví dụ về dao động mà bạn quan sát được trong thực tế
Với một cái thước mỏng đàn hồi, hãy đề xuất phương án tạo ra dao động tự do của thước và mô tả cách làm
Nếu bỏ qua lực cản, chuyển động nào sau đây là dao động tự do:
A. Một con muỗi đang đập cánh
B. Tòa nhà rung chuyển trong trận động đất
C. Mặt trống rung động sau khi gõ
D. Bông hoa rung rinh trong gió nhẹ
Từ đồ thị Hình 1.7, mô tả sự thay đổi li độ của xe theo thời gian
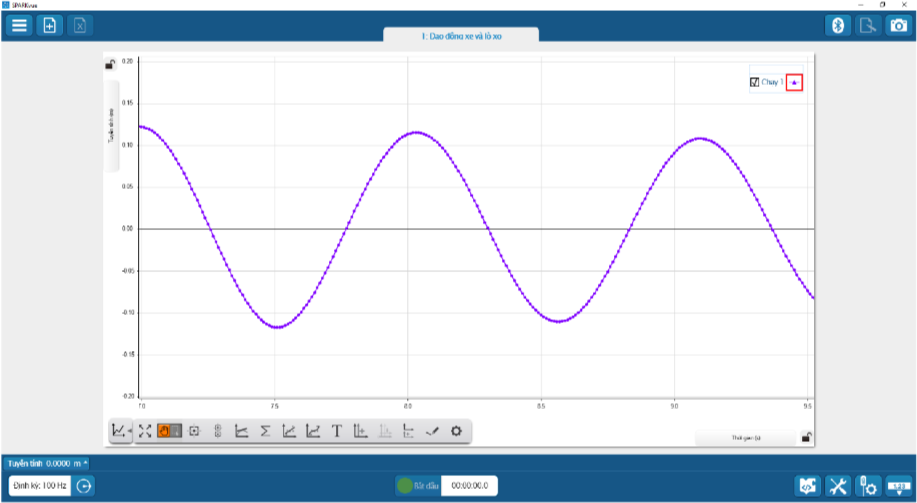
Hình 1.7. Ảnh chụp màn hình một phần đồ thị mô tả dao động của xe
Tìm mối liên hệ giữa chu kì T và tần số f của dao động
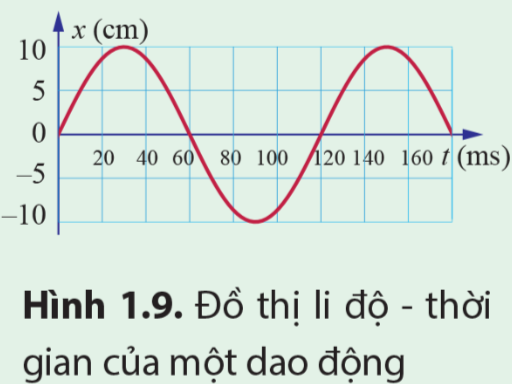
Xác định biên độ, chu kì và tần số của dao động có đồ thị li độ thời gian được biểu diễn ở Hình 1.9
Thế nào là dao động điều hòa?
Tần số góc và tần số của dao động điều hòa có liên hệ như thế nào
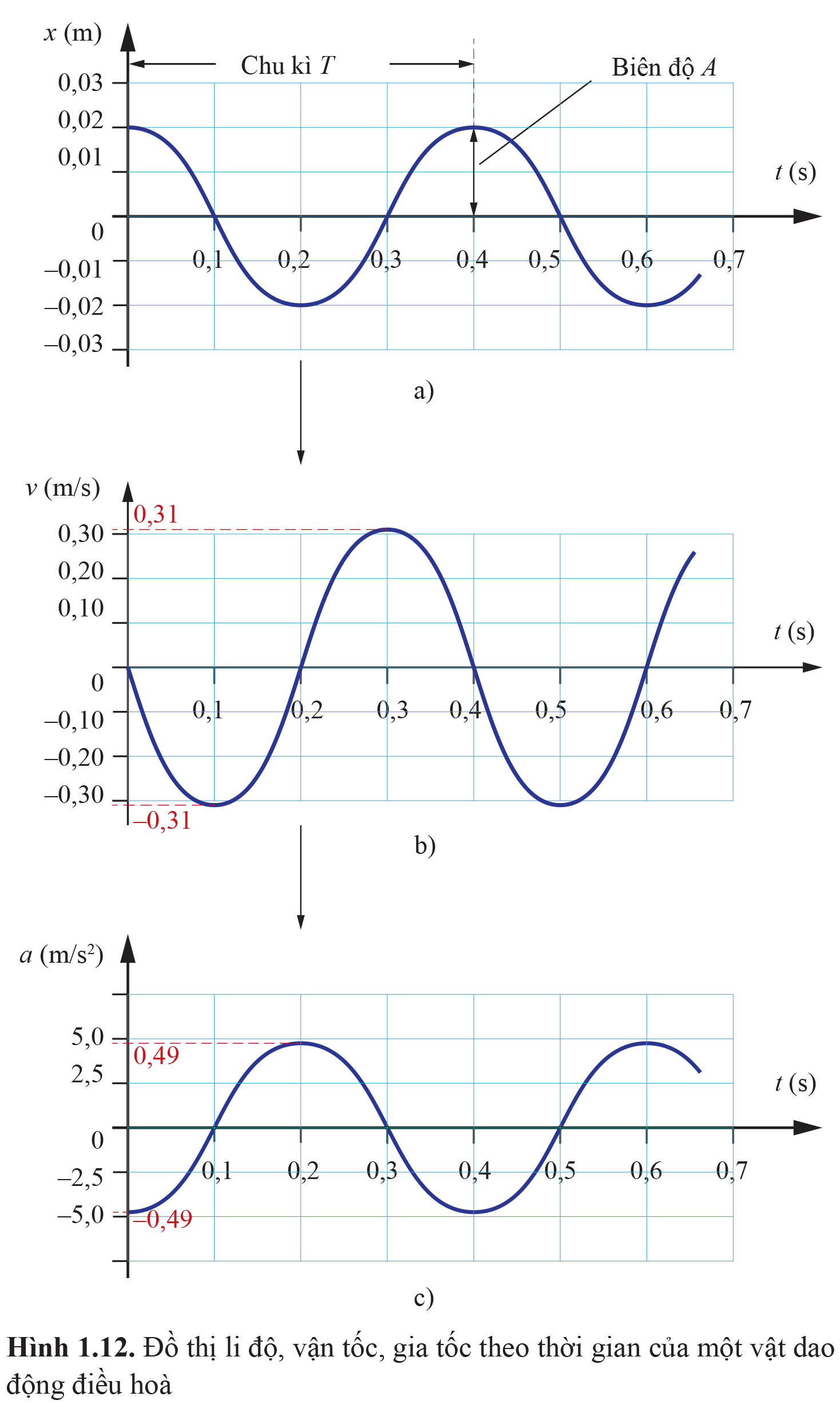
Dựa vào đồ thị Hình 1.12, xác định các đại lượng sau:
a. Tần số góc của dao động.
b. Biên độ của dao động.
c. Vận tốc cực đại của vật dao động.
d. Gia tốc cực đại của vật dao động.

Dựa vào độ dốc của đồ thị li độ - thời gian, ta có thể xác định vận tốc của xe kĩ thuật số tại mỗi thời điểm. Từ các số liệu này có thể vẽ được đồ thị hình sin biểu diễn sự liên hệ giữa vận tốc và thời gian (Hình 1.12b).
Ví dụ, trong Hình 1.12a, độ dốc của đồ thị li độ - thời gian bằng 0, vận tốc bằng 0. Khi t tăng từ 0 s đến 0,2 s, độ dốc âm, vận tốc có giá trị âm. Tại t = 0,2 s, độ dốc bằng 0 một lần nữa. Từ t = 0,2 s đến t = 0,4 s, độ dốc dương, vận tốc có giá trị dương. Độ dốc của đồ thị li độ - thời gian có độ lớn cực đại tại các thời điểm t = 0,1 s; 0,3 s; 0,5 s; …
Bằng cách tương tự, dựa vào độ dốc của đồ thị vận tốc – thời gian ở Hình 1.12b, ta có thể tìm được gia tốc của xe tại mỗi thời điểm và vẽ được đồ thị hình sin như Hình 1.12c.
Dựa vào các đồ thị ở Hình 1.12, tìm:
Các thời điểm gia tốc của xe bằng 0.
Các thời điểm gia tốc của xe cực đại.
Giải thích cách làm.
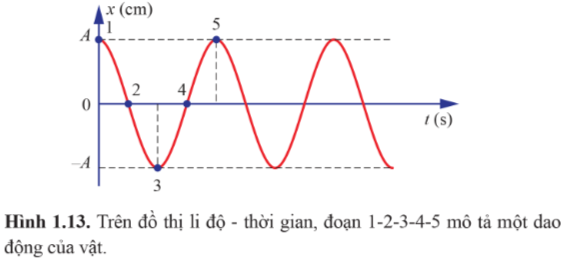
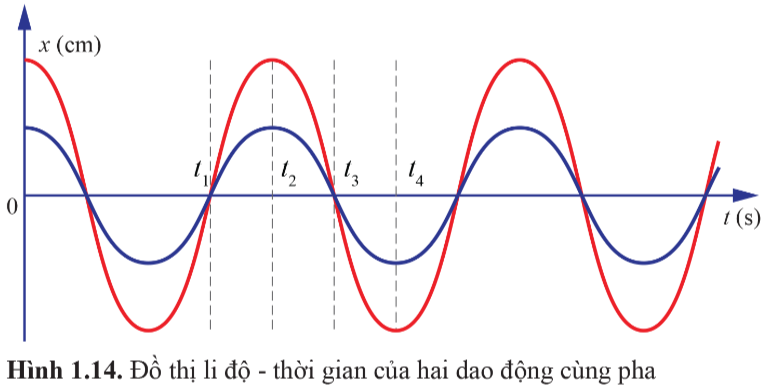
Xác định pha của dao động tại vị trí 3 và vị trí 4
Một vật dao động điều hòa với phương trình li độ: \(x = 5\cos (10\pi t + \frac{\pi }{2})\)(cm). Xác định pha của dao động tại thời điểm \(\frac{1}{{30}}\)s
Mô tả trạng thái của hai vật dao động ở thời điểm t3 và t4 trong đồ thị Hình 1.14
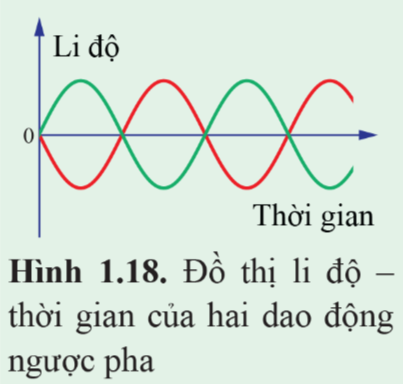
Đồ thị Hình 1.18 biểu diễn hai dao động ngược pha.
Dựa vào đồ thị, xác định độ lệch pha của hai dao động này
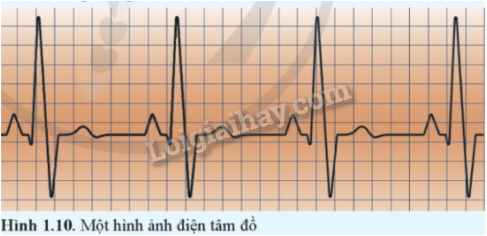
Tim co bóp theo nhịp do được điều khiển bằng một hệ thống các xung điện dẫn truyền trong cơ tim. Máy điện tim ghi nhận những xung điện này và hiển thị dưới dạng đường điện tâm đồ. Đó là những đường gấp khúc, lên xuống biến thiên theo nhịp co bóp của tim.
Dựa vào hình ảnh điện tâm đồ ở Hình 1.10, xác định chu kì đập của tim. Biết rằng mỗi khoảng vuông (theo chiều ngang) tương ứng với khoảng thời gian 0,12 s.
Sự dao động của các vật diễn ra phổ biến trong cuộc sống hàng ngày như: dao động của quả lắc đồng hồ (Hình 1.1a), dao động của cánh chim ruồi để giữ cho cơ thể bay tại chỗ trong không trung khi hút mật (Hình 1.1b). Vậy dao động có đặc điểm gì và được mô tả như thế nào?
Một chất điểm dao động điều hoà có quỹ đạo là một đoạn thằng dài 10 cm. Biên độ dao động của chất điểm là:
A. 5 cm. B. -5cm. C. 10 cm. D. -10cm.
Một chất điểm dao động điều hoà trong 10 dao động toàn phần đi được quãng đường dài 120 cm. Quỹ đạo của dao động có chiều dài là
A. 6 cm. B. 12 cm. C. 3 cm. D. 9 cm.
Một chất điểm dao động điều hoà với phương trình :
\(x = 5\cos \left( {10\pi + \frac{\pi }{3}} \right)\)\(\left( {cm} \right)\). Li độ của vật khi pha dao động bằng \(\left( \pi \right)\) là
A. 5 cm. B. -5cm. C. 2,5 cm. D. -2.5 cm.
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là: \(x = 5\sqrt 3 \cos \)\(x = 5\sqrt 3 \cos \left( {10\pi + \frac{\pi }{3}} \right)\)\(\left( {cm} \right)\) .Tại thời điểm \(t = 1\left( s \right)\) thì li độ của vật bằng:
A. 25cm. B. \( - 5\sqrt 3 \) cm. C. 5 cm, D. \(2,5\sqrt 3 \)cm.
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là: \(x = 6\cos \left( {10\pi t + \frac{\pi }{3}} \right)\)\(\left( {cm} \right)\).Li độ của vật khi pha dao động bằng \(\left( { - \frac{\pi }{3}} \right)\) là:
A. 3 cm B. -3 cm C. 4.24 cm D. -4.24 cm
Một chất điểm M chuyền động đều trên một đường tròn, bán kính R, vận tốc góc . Hình chiều của M trên đường kính là một dao động điều hoà có
A. biên độ R B. biên độ 2R. C. pha ban đầu t D. quỹ đạo 4R
Phương trình dao động của một vật có dạng:\(x = - A\cos \left( {\omega t + \frac{\pi }{3}} \right)\left( {cm} \right)\). Pha ban đầu của dao động là
A. \(\frac{\pi }{3}\) cm B. \( - \frac{\pi }{3}\) cm C. \(\frac{{2\pi }}{3}\) cm D. \( - \frac{{2\pi }}{3}\) cm
Phương trình dao động điều hoà là \(x = 5\cos \left( {2\pi t + \frac{\pi }{3}} \right)\left( {cm} \right)\). Hãy cho biết biên độ, pha ban đầu và pha ở thời điểm t của dao động.
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là:
\(x = 10\cos \left( {\frac{\pi }{3}t + \frac{\pi }{2}} \right)\left( {cm} \right)\)
a) Tính quãng đường vật đi được sau 2 dao động.
b) Tính li độ của vật khi \(t = 6\left( s \right)\).
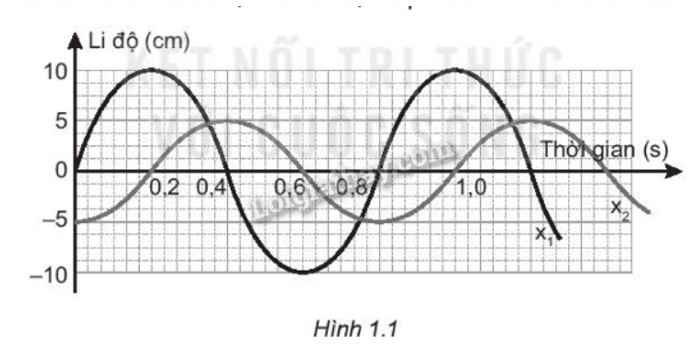
Đồ thị li độ theo thời gian x1, x2, của hai chát điểm dao động điều hoà được mô tả như Hình 1.1. Xác định biên độ và pha ban đầu của mỗi dao động.

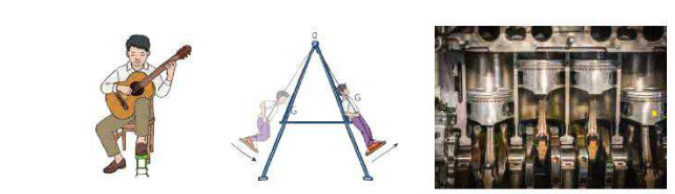






Danh sách bình luận