a) Nhiệt độ cơ thể d $\left( {^\circ C} \right)$ của bệnh nhân theo thời gian h (giờ) trong ngày được ghi trong bảng sau:

 

Ứng với mỗi giờ em đọc được bao nhiêu số chỉ nhiệt độ?

b) Thời gian $t$ (giờ) để một vật chuyển động đều đi hết quãng đường 180 km tỉ lệ nghịch với vận tốc $v$ (km/h) của nó theo công thức $t = \dfrac{{180}}{v}$.

Tính và lập bảng các giá trị tương ứng của $t$ và $v$ lần lượt bằng 10; 20; 30; 60; 180.

Ứng với mỗi giá trị của đại lượng $v$ em tính được bao nhiêu giá trị của đại lượng $t$?

Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y.

Chọn đáp án đúng

Cho hàm số $y = f\left( x \right) = kx$ (k là hằng số, $k \ne 0$). Chọn đáp án đúng.

Cho hai hàm số: $f\left( x \right) =  - 6{x^2} + 12x - 7,g\left( x \right) = 3{x^2} + 6x + 4$

Khẳng định nào sau đây là đúng?

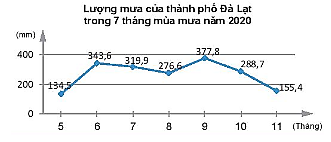
Số liệu về lượng mưa M (mm) trong 7 tháng mùa mưa của thành phố Đà Lạt năm 2020 được biểu diễn  theo số n chỉ số trong tháng có biểu đồ dưới đây.

Quan sát biểu đồ và cho biết lượng mưa ở mỗi tháng là bao nhiêu?

Mô tả các đại lượng là hàm số và biến số trong các mô hình sau:

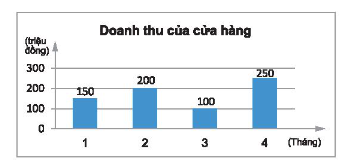
a) Biểu đồ cột chỉ doanh thu $y$ (triệu đồng) của một cửa hàng trong các tháng $x$.

b) Quãng đường $s$ (km) đi được trong khoảng thời gian $t$ (giờ) của một chiếc xe chạy với tốc độ không đổi bằng 40 km/h.

c) Số tiền $y$ (đồng) người mua phải trả cho $x$ quyển vở có giá trị 10 000 đồng/ quyển.

Khi đo nhiệt độ, ta có công thức đổi từ đơn vị độ C (Celsius) sang đơn vị độ F (Fahrenheit) như sau: F = 1,8C + 3,2. Theo em, F có phải làm một hàm số theo biến số C hay không? Giải thích.

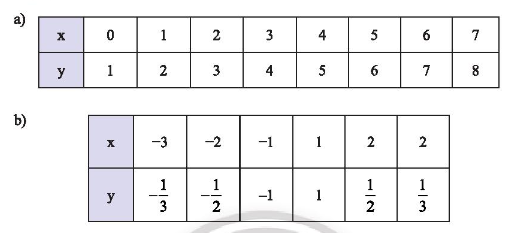
a) Các giá trị tương ứng của hai đại lượng $x$ và $y$ được cho trong bảng sau:

Đại lượng $y$ có phải là hàm số của đại lượng $x$ không?

b) Cho hàm số $y = f\left( x \right) = {x^2}$

- Tính $f\left( 2 \right);f\left( { - 3} \right)$.

- Lập bảng giá trị của hàm số với $x$ lần lượt bằng $- 3; - 2; - 1;0;1;2;3$.

Cho $C = f\left( d \right)$là hàm số mô tả mối quan hệ giữa chu vi $C$ và đường kính $d$ của một đường tròn. Tìm công thức $f\left( d \right)$ và lập bảng giá trị của hàm số ứng với $d$ lần lượt bằng $1;2;3;4$ (theo đơn vị cm).

Các giá trị tương ứng của hai đại lượng $x$ và $y$ được cho trong bảng sau. Trong mỗi trường hợp, hãy cho biết đại lượng $y$ có phải là hàm số của đại lượng $x$ không? Giải thích.

Cho hàm số $y = f\left( x \right) = 3x$

a) Tính $f\left( 1 \right);f\left( { - 2} \right);f\left( {\dfrac{1}{3}} \right)$.

b) Lập bảng các giá trị tương ứng của $y$ khi $x$ lần lượt nhận các giá trị:

$- 3; - 2; - 1;0;1;2;3$.

Cho hàm số $y = f\left( x \right) = {x^2} + 4$. Tính $f\left( { - 3} \right);f\left( { - 2} \right);f\left( { - 1} \right);f\left( 0 \right);f\left( 1 \right)$

Khối lượng m (g) của một thanh sắt có khối lượng riêng là 7,8 kg/dm³ tỉ lệ thuận với thể tích V (cm³) theo công thức m = 7,8V. Đại lượng m có phải là hàm số của đại lượng V không? Nếu có, tính m(10); m(20); m(40); m(50).

Thời gian $t$(giờ) của một vật chuyển động đều trên quãng đường 20 km tỉ lệ nghịch với tốc độ $v$ (km/h) của nó theo công thức $t = \dfrac{{20}}{v}$. Tính và lập bảng các giá trị tương ứng của $t$ với $v$ lần lượt nhận các giá trị 10; 20; 40; 80.

Thanh long là một loại cậy chịu hạn không kén đất, rất thích hợp với điều kiện khí hậu và thổ nhưỡng của tỉnh Bình Thuận. Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng. Với mỗi lượng thanh long loại I được bán ra, người bán sẽ thu được một số tiền tương ứng.

Mối liên hệ giữa hai đại lượng số kilôgam thanh long được bán ra và số tiền người bán thu được thể hiện khái niệm nào trong toán học?

Chu vi y (cm) của hình vuông có độ dài cạnh x (cm) được tính theo công thức y = 4x. Với mỗi giá trị của x, xác định được bao nhiêu giá trị tương ứng của y?

Trong tình huống ở phần mở đầu, hãy cho biết:

a) Số tiền người bán thu được khi lần lượt bán 2 kg thanh long; 3 kg thanh long.

b) Gọi y (đồng) là số tiền người bán thu được khi bán x (kg) thanh long. Với mỗi giá trị của x, ta xác định được bao nhiêu giá trị tương ứng của y.

Cho hai ví dụ về hàm số

Một xe ô tô chạy với tốc độ 60 km/h trong thời gian t (h).

a) Viết hàm số biểu thị quãng đường S(t) (km) mà ô tô đi được trong thời gian t (h).

b) Tính quãng đường S(t) (km) mà ô tô đi được trong thời gian t = 2 (h); t = 3 (h).

Cho hàm số: $f(x) =  - 5{\rm{x}} + 3$. Tính $f(0);f( - 1);f(\frac {1}{2})$

Đại lượng y có phải là hàm số của đại lượng x hay không nếu bảng giá trị tương ứng của chúng được cho bởi mỗi trường hợp sau:

a)

b)

a) Cho hàm số y = 2x + 10. Tìm giá trị của y tương ứng với mỗi giá trị sau của x:

x = -5; x = 0; x = $\dfrac{1}{2}$

b) Cho hàm số y = -2x² + 1. Tìm giá trị của y tương ứng với mỗi giá trị sau của x:

x = -1; x = 0; x = 1; x = $\dfrac{1}{3}$

Cho một thanh kim loại đồng chất có khối lượng riêng 7,8 g/cm³.

a) Viết công thức tính khối lượng m (g) theo thể tích V (cm³). Hỏi m có phải là hàm số của V hay không? Vì sao?

b) Tính khối lượng của thanh kim loại đó khi biết thể tích của thanh kim loại đó là V = 1000 cm³.

Dừa sáp là một trong những đặc sản lạ, quý hiếm và có giá trị dinh dưỡng cao, thường được trồng ở Bến Tre hoặc Trà Vinh. Giá bán mỗi quả dừa sáp là 200 000 đồng.

a) Viết công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (quả) dừa sáp. Hỏi y có phải là hàm số của x hay không? Vì sao?

b) Hãy tính số tiền mà người mua phải trả khi mua 10 quả dừa sáp.

Bác Ninh gửi tiết kiệm 10 triệu đồng ở ngân hàng với kì hạn 12 tháng và không rút tiền trước kì hạn. Lãi suất ngân hàng quy định cho kì hạn 12 tháng là r%/năm.

a) Viết công thức biểu thị số tiền lãi y (đồng) theo lãi suất r%/năm mà bác Ninh nhận được sau khi hết kì hạn 12 tháng. Hỏi y có phải là hàm số của r hay không? Vì sao?

b) Tính số tiền lãi mà bác Ninh nhận được khi hết kì hạn 12 tháng, biết r = 5,6.

Thống kê nhiệt độ $T\left( {^\circ C} \right)$ tại một địa điểm thuộc vùng ôn đới ở một số thời điểm $t\left( h \right)$ trong một ngày được cho bởi bảng sau:

a) Trong các thời điểm trong bảng trên, thời điểm nào có nhiệt độ cao nhất? Thấp nhất?

b) Nhiệt độ $T$ có phải hàm số của thời điểm $t$ hay không? Vì sao?

c) Thời điểm $t$ có phải hàm số của nhiệt độ $T$ hay không? Vì sao?

Một hòn đá rơi xuống hang với quãng đường rơi xuống $h\left( m \right)$ trong thời gian $t$ (giây) được tính bởi công thức $h = 4,9{t^2}.$ Hỏi $h$ có phải hàm số của $t$ hay không? Vì sao?

Giá của chiếc máy tính bảng lúc mới mua là $9\,800\,000$ đồng. Giá trị của chiếc máy tính bảng đó sau khi sử dụng $x$ (năm) được tính bởi công thức:

$V\left( x \right) = 9\,800\,000 - 800\,000x$.

a) Hỏi $V\left( x \right)$ có phải là hàm số của $x$ hay không? Vì sao?

b) Tính $V\left( 3 \right)$ và cho biết $V\left( 3 \right)$ có nghĩa là gì.

c) Sau bao nhiêu năm thì giá trị của chiếc máy tính bảng đó là $5\,000\,000$ đồng?

Cho hàm số $f\left( x \right) = {x^3} - 2.$ Tìm số thích hợp cho ? trong bảng sau:

Cho hàm số $f\left( x \right) = 2 - 3x.$ Trong các phát biểu sau, phát biểu nào đúng?

a) $f\left( { - 1} \right) = 5.$

b) $f\left( 0 \right) =  - 3.$

c) $f\left( {\frac{1}{3}} \right) =  - 1.$

d) $f\left( { - \frac{1}{3}} \right) = 3.$

Cho hàm số $g\left( x \right) = 5{x^2} + 7.$ Bạn Bình nhận định: Luôn tìm được hai số $a$ và $b$ sao cho $a < b$ mà $g\left( a \right) > g\left( b \right).$ Nhận định của bạn Bình đúng hay sai? Vì sao?