Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh ∆OAM = ∆OCN. Từ đó suy ra tứ giác MBND là hình bình hành.
Chứng minh tứ giác MBND có:
• BM // DN (vì AB // CD)
• BM = DN
Do đó, tứ giác MBND là hình bình hành.

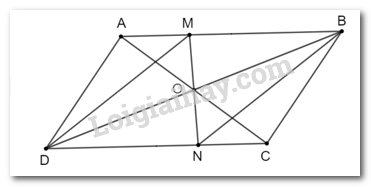
Vì ABCD là hình bình hành nên ta có:
• Hai đường chéo AC và BD cắt nhau tại O nên OA = OC, OB = OD.
• AB // CD nên AM // CN suy ra \(\widehat {OAM} = \widehat {OCN}\) (hai góc so le trong).
Xét ∆OAM và ∆OCN có:
\(\widehat {OAM} = \widehat {OCN}\) (chứng minh trên)
OA = OC (chứng minh trên)
\(\widehat {AOM} = \widehat {CON}\) (hai góc đối đỉnh)
Do đó ∆OAM = ∆OCN (g.c.g).
Suy ra AM = CN (hai cạnh tương ứng)
Mặt khác, AB = CD (chứng minh trên); AB = AM + BM; CD = CN + DN.
Suy ra BM = DN.
Xét tứ giác MBND có:
• BM // DN (vì AB // CD)
• BM = DN (chứng minh trên)
Do đó, tứ giác MBND là hình bình hành.

Các bài tập cùng chuyên đề
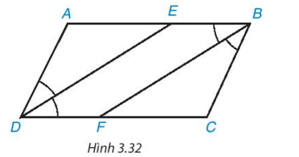
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E và tia phân giác của góc B cắt CD tại F (H.3.32).
a) Chứng minh hai tam giác ADE và CBF là những tam giác cân, bằng nhau.
b) Tứ giác DEBF là hình gì? Tại sao?
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Vì sao?
a) Hình thang có hai cạnh bên song song là hình bình hành.
b) Hình thang có hai cạnh bên bằng nhau là hình bình hành.
c) Tứ giác có hai cạnh đối nào cũng song song là hình bình hành.
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) Hai tứ giác AEFD, AECF là những hình bình hành;
b) EF = AD, AF = EC.
Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:
a) Hai tứ giác AEFD, ABFC là những hình bình hành;
b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.
Cho hình bình hành \(ABCD\), kẻ \(AH\) vuông góc với \(BD\) tại \(H\) và \(CK\) vuông góc với \(BD\) tại \(K\) (Hình 20)
a) Chứng minh tứ giác \(AHCK\) là hình bình hành
b) Gọi \(I\) là trung điểm của \(HK\).Chứng minh \(IB = ID\)

Cho hình bình hành \(ABCD\) (\(AB > BC\)). Tia phân giác của góc \(D\) cắt \(AB\) tại \(E\), tia phân giác của góc \(B\) cắt \(CD\) tại \(F\)
a) Chứng minh \(DE\) // \(BF\)
b) Tứ giác \(DEBF\) là hình gì?
Cho hình bình hành \(ABCD\). Các điểm \(E\), \(F\) thuộc đường chéo \(AC\) sao cho \(AE = EF = FC\). Gọi \(M\) là trung điểm của \(BF\) và \(CD\), \(N\) là giao điểm của \(DE\) và \(AB\). Chứng minh rằng:
a) \(M\), \(N\) theo thứ tự là trung điểm của \(CD\), \(AB\)
b) \(EMFN\) là hình bình hành
Cho tứ giác ABCD có \(\widehat {DAB} = \widehat {BC{\rm{D}}};\widehat {ABC} = \widehat {C{\rm{D}}A}\). Kẻ tia Ax là tia đối của tia AB. Chứng minh:
a) \(\widehat {ABC} + \widehat {DAB} = {180^o}\)
b) \(\widehat {xA{\rm{D}}} = \widehat {ABC};AD//BC\)
c) Tứ giác ABCD là hình bình hành.
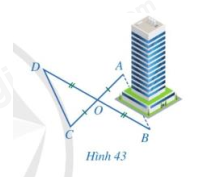
Để đo khoảng cách giữa hai vị trí A, B ở hai phía của một tòa nhà mà không thể đo trực tiếp được, người ta làm như sau: Chọn các vị trí O, C, D sao cho O không thuộc đường thẳng AB; khoảng cách CD là đo được; O là trung điểm của cả AC và BD (hình 43). Người ta đo được CD = 100 m và khẳng định AB = 100 m. Em hãy giải thích vì sao AB = 100m.
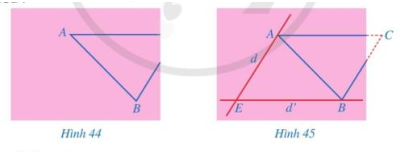
Bạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác ở phái góc (Hình 44). Bạn Hoa đó bạn Hùng: Không vẽ lại tam giác ABC, làm thế nào tính được độ dài đoạn thẳng AC, BC và số đo góc ACB?
Bạn Hùng làm như sau:
- Qua điểm A kẻ đường thẳng d song song với BC; qua điểm B kẻ đường thẳng d’ song song với AC.
- Gọi E là giao điểm của d và d’.
- Đo độ dài các đoạn thẳng AE, BE và đo góc AEB. Từ đó, tính được độ dài các đoạn thẳng AC, BC và số đo góc ACB (hình 45).
Em hãy giải thích cách làm của bạn Hùng.
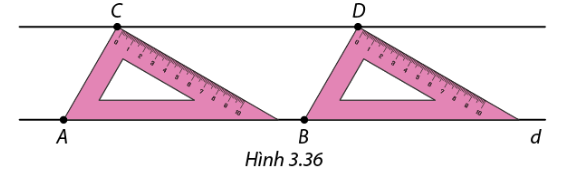
Trong Hình 3.36, Nam di chuyển thước ê ke dọc theo đường thẳng d sao cho cạnh huyền của thước luôn nằm trên d. Khi đỉnh góc \(60^\circ \) lần lượt ở vị trí điểm \(C\) và \(D.\) Nối hai điểm \(C\) và \(D,\) Nam được một đường thẳng song song với d. Em hãy giải thích vì sao?
Cho ABCD là hình bình hành. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AB,BC,CD và AD. Chứng minh rằng:
a) AMPD là hình bình hành
b) AN song song CQ
c) MNPQ là hình bình hành.
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) Hai tứ giác AEFD, AECF là những hình bình hành.
b) EF = AD, AF = EC.
Cho tam giác nhọn ABC có trực tâm H. Vẽ các đường thẳng d vuông góc với AB tại B, d’ vuông góc với AC tại C, d và d’ cắt nhau tại N. Chứng mình rằng:
a) Tứ giác BHCN là hình bình hành.
b) HN đi qua trung điểm I của đoạn thẳng BC.
Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD.
a) Chứng minh rằng tứ giác AHCK là hình bình hành.
b) Gọi M là giao điểm của AK và BC, N là giao điểm của CH và AD. Chứng minh \(AN = CM.\)
c) Gọi O là trung điểm của HK. Chứng minh M, O, N thẳng hàng.
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho \(BM = DN = \frac{1}{3}BD\).
a) Chứng minh \(\Delta AMB = \Delta CND\).
b) Chứng minh rằng tứ giác AMCN là hình bình hành.
c) Gọi O là giao điểm của AC và BD, I là giao điểm của AM và BC. Chứng minh rằng \(AM = 2MI\).
d) Gọi K là giao điểm của CN và AD. Chứng minh I và K đối xứng với nhau qua O.
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.
Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:
a) AN = CM.
b) \(\widehat {AMC} = \widehat {ANC}.\)
Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:
a) Hai tứ giác AEFD, ABFC là những hình bình hành.
b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.
Cho hình bình hành ABCD. Gọi H, K lần lượt là các chân đường cao kẻ từ đỉnh A, C xuống BD (H.3.28).

Chứng minh rằng:
a) ∆ADH = ∆CBK.
b) Tứ giác AHCK là hình bình hành.
c) AC đi qua trung điểm O của HK.
Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy của nó.
Hãy chọn câu sai.
-
A.
Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
-
B.
Hình bình hành có hai góc đối bằng nhau.
-
C.
Hình bình hành có hai đường chéo vuông góc với nhau.
-
D.
Hình bình hành có hai cặp cạnh đối song song.
Cho tam giác \(ABC\) và \(H\) là trực tâm. Các đường thẳng vuông góc với \(AB\) tại \(B\), vuông góc với \(AC\) tại \(C\) cắt nhau ở \(D\). Biết \(\widehat {BAC} = {50^o}\), số đo góc \(BDC\) là:
-
A.
\(50^{o}\);
-
B.
\(100^{o}\);
-
C.
\(150^{o}\);
-
D.
\(130^{o}\);
Cho tứ giác \(ABCD\). Gọi \(E\), \(F\) lần lượt là trung điểm của \(AB\) và \(CD\); \(M\), \(N\), \(P\), \(Q\) lần lượt là trung điểm các cạnh \(AF\), \(EC\), \(BF\), \(DE\) và \(FN = \frac{1}{2}DE;\,FN\parallel DE\); \(EM = \frac{1}{2}BF;\,EM\parallel BF\). Khi đó \(MNPQ\) là hình gì? Khẳng định nào sau đây là đúng nhất?
-
A.
Hình bình hành
-
B.
Hình thang vuông
-
C.
Hình thang cân
-
D.
Hình thang
Chọn câu đúng:
-
A.
Hình bình hành là tứ giác có các góc bằng nhau.
-
B.
Hình bình hành là tứ giác có hai cặp cạnh đối song song.
-
C.
Hình bình hành là tứ giác có hai cạnh đối song song.
-
D.
Hình bình hành là hình thang có hai cạnh bên bằng nhau.







Bình luận