Trong không gian Oxyz, cho hai đường thẳng d: $\frac{{x + 2}}{1} = \frac{{y + 3}}{2} = \frac{{z - 3}}{{ - 2}}$ và $d':\left\{ \begin{array}{l}x = 1 - t\\y =  - 2 + t\\z = 2t\end{array} \right.$.

a) Xác định vị trí tương đối của hai đường thẳng d và d’.

b) Tính góc giữa d và d’.

Trong không gian Oxyz, tính góc giữa trục Oz và đường thẳng $\Delta :\frac{{x - 3}}{1} = \frac{{y + 1}}{2} = \frac{{z - 1}}{{ - 2}}$.

Trong không gian Oxyz, tính góc giữa hai đường thẳng ${\Delta _1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 - t\\z = 2 + 3t\end{array} \right.$ và ${\Delta _2}:\frac{{x - 2}}{{ - 1}} = \frac{{x + 1}}{1} = \frac{{z - 2}}{2}$.

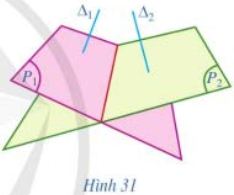
Cho hai mặt phẳng $\left( {{P_1}} \right)$ và $\left( {{P_2}} \right)$. Lấy hai đường thẳng ${\Delta _1},{\Delta _2}$ sao cho ${\Delta _1} \bot \left( {{P_1}} \right),$ ${\Delta _2} \bot \left( {{P_2}} \right)$ (Hình 31).

\

a) Nêu cách xác định góc giữa hai đường thẳng ${\Delta _1},{\Delta _2}$.

b) Góc đó có phụ thuộc vào việc chọn hai đường thẳng ${\Delta _1},{\Delta _2}$ như trên không?

Tính góc giữa hai đường thẳng ${\Delta _1},{\Delta _2}$ trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):

a) ${\Delta _1}:\left\{ \begin{array}{l}x =  - 1 + {t_1}\\y = 4 + \sqrt 3 {t_1}\\z = 0\end{array} \right.$ và ${\Delta _2}:\left\{ \begin{array}{l}x =  - 1 + \sqrt 3 {t_2}\\y = 4 + {t_2}\\z = 5\end{array} \right.$ (${t_1},{t_2}$ là tham số);

b) ${\Delta _1}:\left\{ \begin{array}{l}x =  - 1 + 2t\\y = 3 + t\\z = 4 - t\end{array} \right.$ (t là tham số) và ${\Delta _2}:\frac{{x + 1}}{3} = \frac{{y - 1}}{1} = \frac{{z - 4}}{{ - 2}}$;

c) ${\Delta _1}:\frac{{x + 3}}{1} = \frac{{y - 2}}{1} = \frac{{z - 1}}{{ - 1}}$ và ${\Delta _2}:\frac{{x + 2}}{{ - 1}} = \frac{{y - 2}}{3} = \frac{{z - 4}}{1}$.

Tính góc giữa hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$, biết: ${\Delta _1}:\left\{ \begin{array}{l}x = 1 + {t_1}\\y = 2 - \sqrt 2 {t_1}\\z = 3 + {t_1}\end{array} \right.$ và ${\Delta _2}:\left\{ \begin{array}{l}x =  - 3 + {t_2}\\y = 1 + {t_2}\\z = 5 - \sqrt 2 {t_2}\end{array} \right.$ ( là tham số) (làm tròn kết quả đến hàng đơn vị của độ).

Cho hai đường thẳng $d$ và $d'$ có vectơ chỉ phương lần lượt là $\vec a = \left( {2;1;3} \right)$ và $\vec a' = \left( {3;2; - 8} \right)$.

a) Nhắc lại định nghĩa góc giữa hai đường thẳng $d$ và $d'$ trong không gian.

b) Vectơ $\vec b = \left( { - 2;; - 1; - 3} \right)$ có phải là một vectơ chỉ phương của $d$ không?

c) Giải thích tại sao ta lại có đẳng thức $\cos \left( {d,d'} \right) = \left| {\cos \left( {\vec a,\vec a'} \right)} \right| = \left| {\cos \left( {\vec b,\vec a'} \right)} \right|$.

d) Nêu cách tìm côsin của góc giữa hai đường thẳng theo côsin của góc giữa hai vectơ chỉ phương của hai đường thẳng đó.

Tính góc giữa hai đường thẳng $d$ và $d'$ trong mỗi trường hợp sau:

a) $d:\frac{{x - 7}}{3} = \frac{y}{5} = \frac{{z - 11}}{4}$ và $d':\frac{{x - 3}}{2} = \frac{{y + 6}}{5} = \frac{{z - 1}}{{ - 4}}.$

b) $d:\frac{{x + 9}}{3} = \frac{{y + 4}}{6} = \frac{{z + 1}}{6}$ và $d':\left\{ \begin{array}{l}x = 9 - 10t\\y = 7 - 10t\\z = 15 + 5t\end{array} \right.$.

c) $d:\left\{ \begin{array}{l}x = 23 + 2t\\y = 57 + t\\z = 19 - 5t\end{array} \right.$ và $d':\left\{ \begin{array}{l}x = 24 + t'\\y = 6 + t'\\z = t'\end{array} \right.$.

Cho đường thẳng $d$ có vectơ chỉ phương là $\vec a = \left( {{a_1};{a_2};{a_3}} \right)$ và mặt phẳng $\left( P \right)$ có vectơ pháp tuyến $\vec n = \left( {{n_1};{n_2};{n_3}} \right)$. Biết $d$ cắt $\left( P \right)$ tại điểm $N$ và hình chiếu vuông góc của $d$ lên $\left( P \right)$ là đường thẳng $d'$. Qua $N$ vẽ đường thẳng $\Delta$ vuông góc với $\left( P \right)$ (hình dưới đây).

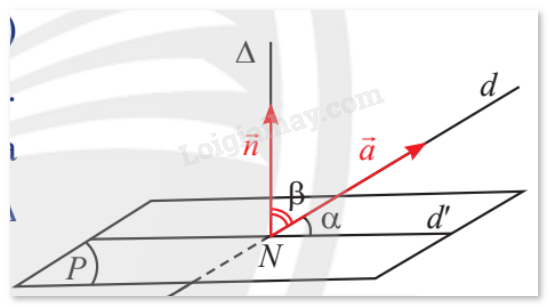
a) Nhắc lại định nghĩa góc giữa đường thẳng và mặt phẳng trong không gian.

b) Có nhận xét gì về số đo hai góc $\alpha  = \left( {d,d'} \right)$; $\beta  = \left( {\Delta ,d} \right)$?

c) Giải thích tại sao ta lại có đẳng thức $\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|$.

Tính góc giữa hai đường thẳng $d:\frac{{x - 3}}{2} = \frac{{y + 5}}{4} = \frac{{z - 7}}{2}$ và $d':\frac{{x - 1}}{3} = \frac{{y + 7}}{3} = \frac{{z - 12}}{6}$.

Cho đường thẳng $\Delta$ có phương trình tham số $\left\{ \begin{array}{l}x = at\\y = bt\\z = ct\end{array} \right.$ với ${a^2} + {b^2} + {c^2} > 0$.

Côsin của góc giữa đường thẳng $\Delta$ và trục $Oz$ bằng:

A. $\frac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$.

B. $\frac{{\left| a \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$.

C. $\frac{{\left| b \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$.

D. $\frac{{\left| c \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$.

Cho đường thẳng $\Delta$ có phương trình tham số $\left\{ \begin{array}{l}x = at\\y = bt\\z = ct\end{array} \right.$ với ${a^2} + {b^2} + {c^2} > 0$.

Sin của góc giữa đường thẳng $\Delta$ và mặt phẳng $\left( {Oyz} \right)$ bằng:

A. $\frac{{\left| {a + b + c} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$.

B. $\frac{{\left| a \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$.

C. $\frac{{\left| b \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$.

D. $\frac{{\left| c \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$.

Tính góc giữa hai đường thẳng ${\Delta _1},{\Delta _2}$ trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ nếu cần):

a) ${\Delta _1}:\left\{ \begin{array}{l}x = 3 + 2{t_1}\\y =  - 2 + {t_1}\\z = 0\end{array} \right.$ và ${\Delta _2}:\left\{ \begin{array}{l}x = 7 + {t_2}\\y =  - 3 - {t_2}\\z = 2{t_2}\end{array} \right.$ (${t_1},{t_2}$ là tham số);

b) ${\Delta _1}:\left\{ \begin{array}{l}x = 3 + t\\y = 5 - 2t\\z = 7 - 2t\end{array} \right.$ (với $t$ là tham số) và ${\Delta _2}:\frac{{x + 4}}{2} = \frac{{y + 6}}{2} = \frac{{z - 10}}{{ - 1}}$;

c) ${\Delta _1}:\frac{{x + 1}}{{ - 1}} = \frac{{y + 4}}{2} = \frac{{z - 5}}{{ - 3}}$ và ${\Delta _2}:\frac{x}{2} = \frac{{y - 3}}{{ - 1}} = \frac{{z + 2}}{{ - 1}}$.

Tính góc giữa đường thẳng $\Delta$ và mặt phẳng $\left( P \right)$ trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):

a) $\Delta :\left\{ \begin{array}{l}x = 18 - \sqrt 3 t\\y = 11\\z = 5 + t\end{array} \right.$ (với $t$ là tham số) và $\left( P \right):x - \sqrt 3 y - z - 3 = 0$;

b) $\Delta :\frac{{x - 8}}{2} = \frac{{y - 7}}{{ - 3}} = \frac{{z - 6}}{3}$ và $\left( P \right):3x - 4y + 5z - 6 = 0$.

Tính góc giữa hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$ (làm tròn kết quả đến hàng đơn vị của độ), biết ${\Delta _1}:\left\{ \begin{array}{l}x = 8 + \sqrt 2 {t_1}\\y = 9 - {t_1}\\z = 10 + {t_1}\end{array} \right.$ và ${\Delta _2}:\left\{ \begin{array}{l}x =  - 7 + {t_2}\\y =  - 9 + \sqrt 2 {t_2}\\z = 11 - {t_2}\end{array} \right.$ (${t_1},{t_2}$ là tham số).

Trong không gian Oxyz, tính góc giữa hai đường thẳng:

$\Delta :\frac{{x - 2}}{1} = \frac{{y + 2}}{{ - 1}} = \frac{z}{2}$ và $\Delta ':\left\{ \begin{array}{l}x = 3 + 2t\\y =  - 1 + t\\z = 3 + t\end{array} \right.$

Trong không gian Oxyz, côsin của góc giữa hai đường thẳng $\Delta :\left\{ \begin{array}{l}x = 1 + 2t\\y =  - 1 + t\\z =  - 2 + t\end{array} \right.$ và $\Delta ':\frac{{x + 2}}{1} = \frac{{y + 3}}{2} = \frac{{z - 1}}{{ - 5}}$ bằng

A. $\frac{{\sqrt 5 }}{{30}}$.

B. $\frac{{ - \sqrt 5 }}{{30}}$.

C. $\frac{{3\sqrt 5 }}{{10}}$.

D. $\frac{{ - 3\sqrt 5 }}{{10}}$.

Trong không gian Oxyz, tính góc giữa hai đường thẳng d và d' trong các trường hợp sau:

a) $d:\frac{x}{3} = \frac{y}{4} = \frac{z}{5}$ và $d':\frac{{x - 1}}{4} = \frac{y}{2} = \frac{{z + 1}}{2}$

b) $d:\frac{x}{2} = \frac{y}{{ - 4}} = \frac{z}{5}$ và $d':\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = 2 - t\;\\y = 3 + 2t\;\\z = 2t\end{array}\end{array}} \right.$ $(t \in \mathbb{R})$

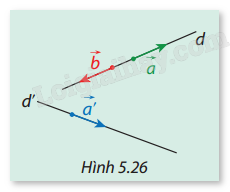
Cho hai vectơ ngược hướng $\vec a$ và $\vec b$ là hai vectơ chỉ phương của đường thẳng $d$ và $\vec a'$ là vectơ chỉ phương của đường thẳng $d'$(Hình 5.26). Cho biết $(d,d') = {45^{^\circ }}$. Hãy tính số đo của hai góc: $\left( {\vec a,\vec a'} \right)$ và $(\vec b,\vec a')$. Từ đó chỉ ra mối quan hệ giữa hai góc $(d,d')$ và $(\vec a,\vec a')$, giữa $\cos (d,d')$ và $\cos (\vec a,\vec a')$.

Tính góc giữa đường thẳng $d:\frac{{x + 3}}{2} = \frac{{y - 1}}{1} = \frac{{z - 2}}{1}$ với các trục tọa độ Ox, Oy, Oz.

Tính góc giữa các cặp đường thẳng sau:

a) $d:\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y =  - 1 + t\,\,\,\,\,\,\,\,\,\,t \in \mathbb{R}}\\{z = 3 + 4t}\end{array}} \right.\quad {\rm{và}}\quad d':\left\{ {\begin{array}{*{20}{l}}{x = 2 - t'}\\{y =  - 1 + 3t'\,\,\,\,\,t'\, \in \mathbb{R}}\\{z = 4 + 2t'}\end{array}} \right.$

b) $d:\frac{x}{1} = \frac{y}{2} = \frac{{z - 2}}{2}\quad {\rm{và }}\quad d':\left\{ {\begin{array}{*{20}{l}}{x = 3 + t'}\\{y =  - 1 + t'\,\,\,\,\,t'\, \in \mathbb{R}}\\{z = 1}\end{array}} \right.$.

c) $d:\frac{{x - 1}}{{ - 2}} = \frac{y}{3} = \frac{{z + 2}}{6}\quad {\rm{và }}\quad d':\frac{x}{{12}} = \frac{{y + 1}}{2} = \frac{z}{3}$.

Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d: $\frac{{x - 3}}{1} = \frac{{y + 1}}{2} = \frac{{z - 5}}{3}$ và d’: $\left\{ \begin{array}{l}x = 2 + 5t\\y = 1 + 2t\\z = 4 - 3t\end{array} \right.$. Góc giữa d và d’ bằng

Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d: $\frac{x}{1} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 1}}{2}$ và d’: $\frac{{x + 1}}{{ - 1}} = \frac{y}{1} = \frac{{z - 3}}{1}$. Góc giữa d và d’ bằng

Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d: $\frac{{x + 3}}{2} = \frac{{y - 1}}{1} = \frac{{z - 2}}{1}$. Cosin góc giữa đường thẳng d và trục Ox là

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d: $\frac{x}{3} = \frac{{y + 1}}{{ 2}} = \frac{{z - 1}}{2}$ và d’ là giao tuyến của hai mặt phẳng (P): x + 2y – z + 1 = 0 và (Q): 2x + 3z - 2 = 0. Góc giữa d và d’

Trong không gian với hệ trục tọa độ Oxyz, đường băng của một sân bay thuộc trục Ox. Một máy bay sau khi chạy đà trên đường băng đó đã cất cánh tại điểm A(2;0;0) với vận tốc không đổi trong khoảng thời gian ngắn ban đầu, vectơ vận tốc $\overrightarrow v  = (2;0;1)$. Hỏi trong khoảng thời gian ngắn nói trên, máy bay chuyển động trên đường thẳng nào và góc cất cánh của máy bay gần với giá trị nào sau đây nhất?

Trong không gian với hệ trục tọa độ Oxyz, hai con đường tại một nút giao thông tương ứng thuộc hai đường thẳng d: $\frac{{x - 1}}{1} = \frac{{y + 1}}{2} = \frac{z}{1}$ và d’: $\frac{{x + 1}}{3} = \frac{{y - 2}}{1} = \frac{{z + 1}}{4}$. Tại nút giao thông nói trên, hai con đường tạo với nhau một góc gần với giá trị nào nhất trong các giá trị sau?

Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-1). Góc giữa hai đường thẳng AB và CD bằng bao nhiêu độ?

Cho hai đường thẳng $d:\frac{{x - 2}}{1} = \frac{{y + 3}}{2} = \frac{{z - 6}}{2}$ và $d':\left\{ {\begin{array}{*{20}{l}}{x = 1 - 2t}\\{y = 2 - 3t}\\{z = 2 - 6t}\end{array}} \right.$ (với $t \in \mathbb{R}$). Khi đó $\cos (d,d')$ bằng:

A. $\frac{{20}}{{21}}$.

B. $\frac{4}{{21}}$.

C. $- \frac{4}{{21}}$.

D. $- \frac{{20}}{{21}}$.

Góc giữa đường thẳng $d:\frac{x}{1} = \frac{{y - 1}}{2} = \frac{z}{1}$ và mặt phẳng $(\alpha ): 4x + 3y + 5z - 4 = 0$ bằng:

A. ${30^\circ }$

B. ${120^\circ }$

C. ${60^\circ }$

D. ${150^\circ }$

Trong không gian Oxyz, cho hai đường thẳng ${d_1}:\frac{x}{{ - 1}} = \frac{{y + 1}}{2} = \frac{z}{2}$, ${d_1}:\left\{ \begin{array}{l}x = 2t\\y = 1\\z = 1 - t\end{array} \right.$. Gọi $\varphi$ là góc giữa hai đường thẳng ${d_1}$ và ${d_2}$. Giá trị $\cos \varphi$ có dạng $\frac{{a\sqrt c }}{b}$. Tính giá trị biểu thức P = b – 3a + c.