Cho hình lập phương ABCD.A’B’C’D’. Chứng minh rằng \(\overrightarrow {A'C} .\overrightarrow {B'D'} = 0\).
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Sử dụng kiến thức về tích vô hướng của hai vectơ trong không gian để tính: Cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Khi đó, \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a \cdot \overrightarrow b = 0\)
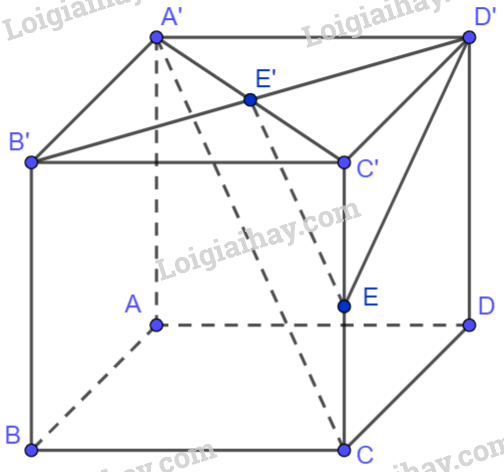
Giả sử cạnh của hình lập phương ABCD.A’B’C’D’ bằng 1. Khi đó, \(A'C' = B'D' = \sqrt 2 \)
Gọi E’ là giao điểm của hai đường chéo A’C’ và B’D’ của hình vuông A’B’C’D’. Khi đó, E’ là trung điểm của A’C’ và B’D’. Suy ra \(\overrightarrow {B'D'} = 2\overrightarrow {E'D'} \) và \(E'D' = \frac{{\sqrt 2 }}{2}\).
Gọi E là trung điểm của CC’. Mà E’ là trung điểm của A’C’ nên EE’ là đường trung bình của tam giác A’C’C. Do đó, \(\overrightarrow {A'C} = 2\overrightarrow {E'E} \) và \(E'E = \frac{1}{2}A'C\)
Áp dụng định lí Pythagore vào \(\Delta \)A’C’C vuông tại C’ có: \(A'C = \sqrt {A'C{'^2} + C'{C^2}} = \sqrt {2 + 1} = \sqrt 3 \)\( \Rightarrow E'E = \frac{{\sqrt 3 }}{2}\)
Áp dụng định lí Pythagore vào \(\Delta \)D’C’E vuông tại C’ có:
\(ED{'^2} = C'D{'^2} + C'{E^2} = 1 + \frac{1}{4} = \frac{5}{4}\)
Vì \(E'D{'^2} + E'{E^2} = \frac{1}{2} + \frac{3}{4} = \frac{5}{4} = ED{'^2}\) nên \(\Delta \)E’D’E vuông tại E’. Do đó, \(\overrightarrow {E'E} \bot \overrightarrow {E'D'} \)
Ta có: \(\overrightarrow {A'C} .\overrightarrow {B'D'} = 2.\overrightarrow {E'E} .2.\overrightarrow {E'D'} \)\( = 0\) (đpcm)
Các bài tập cùng chuyên đề
Như đã biết, nếu có một lực \(\overrightarrow F \) tác động vào một vật tại điểm M và làm cho vật đó di chuyển một quãng đường MN thì công A sinh ra được tính theo công thức \(A = \overrightarrow F .\overrightarrow {MN} \), trong đó lực F có độ lớn tính bằng Newton, quãng đường MN tính bằng mét và công A tính bằng Jun (H.2.28). Do đó, nếu dùng một lực \(\overrightarrow F \) có độ lớn không đổi để làm một vật di chuyển một quãng đường không đổi thì công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật. Hãy giải thích vì sao. Kết quả trên có thể được áp dụng như thế nào khi kéo (hoặc đẩy) các vật nặng?
Trong Ví dụ 10, hãy tính các tích vô hướng \(\overrightarrow {AS} .\overrightarrow {BD} \) và \(\overrightarrow {AS} .\overrightarrow {CD} \)
Hãy nhắc lại công thức xác định tích vô hướng của hai vectơ trong mặt phẳng.
Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) có cùng độ dài bằng 1. Biết rằng góc giữa hai vectơ đó là \({45^0}\), hãy tính:
a) \(\overrightarrow a .\overrightarrow b \);
b) \(\left( {\overrightarrow a + 3\overrightarrow b } \right).\left( {\overrightarrow a - 2\overrightarrow b } \right)\)
c) \({\left( {\overrightarrow a + \overrightarrow b } \right)^2}\).
Cho tứ diện đều ABCD có độ dài cạnh bằng a, gọi M là trung điểm của đoạn thẳng CD. Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AM} \) bằng
A. \(\frac{{{a^2}}}{4}\).
B. \(\frac{{{a^2}}}{2}\).
C. \(\frac{{{a^2}}}{3}\).
D. \({a^2}\).
Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\). Gọi \(\overrightarrow n = \left( {A;B;C} \right)\) là một vectơ pháp tuyến của \(\left( \alpha \right)\) và \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) là một điểm thuộc \(\left( \alpha \right)\).
a) Một điểm M(x; y; z) thuộc \(\left( \alpha \right)\) khi và chỉ hai vectơ \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \) có mối quan hệ gì?
b) Một điểm M(x; y; z) thuộc \(\left( \alpha \right)\) khi và chỉ khi tọa độ của nó thỏa mãn hệ thức nào?
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính
a.\(\overrightarrow {A'B} .\overrightarrow {D'C'} ;\overrightarrow {D'A} .\overrightarrow {BC} \)
b,Các góc \(\left( {\overrightarrow {A'D} ,\overrightarrow {B'C'} } \right);\left( {\overrightarrow {AD',} \overrightarrow {BD} } \right)\)
Trong không gian với hệ tọa độ Oxyz, cho các vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\). Hãy biểu diễn các vecto \(\overrightarrow u ,\overrightarrow v \) theo ba vecto đơn vị \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) và tính tích vô hướng \(\overrightarrow u .\overrightarrow v \)
Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow a = (0;1;1)\) và \(\overrightarrow b = ( - 1;1;0)\). Góc giữa hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) bằng:
A. \(60^\circ \)
B. \(120^\circ \)
C. \(150^\circ \)
D. \(30^\circ \)
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AA’ và CC’. Tính góc giữa hai vecto \(\overrightarrow {MN} \) và \(\overrightarrow {AD'} \)
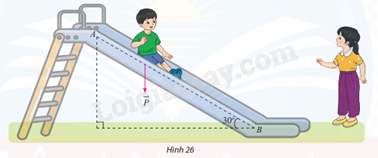
Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là \(30^\circ \) (Hình 26).
a) Tính độ lớn của trọng lực \(\overrightarrow P = m\overrightarrow g \) tác dụng lên em nhỏ, cho biết vectơ gia tốc rơi tự do \(\overrightarrow g \) có độ lớn 9,8\(m/{s^2}\)
b) Cho biết công A (J) sinh bởi một lực \(\overrightarrow F \) có độ dịch chuyển \(\overrightarrow d \) được tính bởi công thức \(A = \overrightarrow F .\overrightarrow d \). Hãy tính công sinh bởi trọng lực \(\overrightarrow P \) khi em nhỏ trượt hết chiều dài cầu trượt.
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1.
a) Tính các tích vô hướng: \(\overrightarrow {AB} .\overrightarrow {A'C'} \), \(\overrightarrow {AB} .\overrightarrow {CC'} \)
b) Tính góc \((\overrightarrow {AC} .\overrightarrow {AC'} )\) (kết quả làm tròn đến phút)
Trong không gian, cho \(\overrightarrow u \) và \(\overrightarrow v \) thoả mãn \(|\overrightarrow u | = 2\) , \(|\overrightarrow v | = 3\). Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \), \(\overrightarrow {AC} = \overrightarrow v \) (Hình 24). Giả sử \(\widehat {BAC} = 60^\circ \)
a) Tính góc \((\overrightarrow u ,\overrightarrow v )\)
b) Trong mặt phẳng (ABC), tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \)
Cho hình lập phương ABCD.A′B′C′D′. Xác định góc \((\overrightarrow {AC} ,\overrightarrow {B'D'} ),(\overrightarrow {A'A} ,\overrightarrow {CB'} )\)
a) Nhắc lại định nghĩa góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong mặt phẳng.
b) Làm thế nào để định nghĩa góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong không gian?
Cho A(2; –1; 1), B(–1; 3; –1), C(5; –3; 4). Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {BC} \) có giá trị là
A. 48.
B. –48.
C. 52.
D. –52.
Cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) tạo với nhau góc \(60^\circ \). Biết rằng \(|\overrightarrow u | = 2\) và \(|\overrightarrow v | = 4\). Tính \(|\overrightarrow u + \overrightarrow v |\)
Cho tứ diện đều ABCD có cạnh bằng 2a. Tích vô hướng \(\overrightarrow {BA} .\overrightarrow {BC} \) bằng:
Công thức tính tích vô hướng của 2 vecto là?
Cho hai vecto \(\overrightarrow u = (2; - 1;3)\), \(\overrightarrow v = ( - 3;4;1)\). Tích \(\overrightarrow u .\overrightarrow v \) bằng:
Cho hai vecto \(\overrightarrow u = (1;4;2)\), \(\overrightarrow v = ( - 1;3;0)\). Tích \(\overrightarrow u .\overrightarrow v \) bằng:
Trong mặt phẳng tọa độ Oxyz, cho hai vecto \(\overrightarrow u = \overrightarrow i + 3\overrightarrow j + 2\overrightarrow k \), \(\overrightarrow v = 2\overrightarrow i + \overrightarrow j + 5\overrightarrow k \). Tích \(\overrightarrow u .\overrightarrow v \) bằng:
Cho hình hộp \(ABCD.A'B'C'D'\) có tất cả các cạnh bằng \(a\) và cho biết \(\widehat {BAD} = \widehat {BAA'} = \widehat {DAA'} = {60^ \circ }\). Tính các tích vô hướng sau:
a) \(\overrightarrow {AB} .\overrightarrow {AD} \);
b) \(\overrightarrow {DA} .\overrightarrow {DC} \);
c) \(\overrightarrow {AA'} .\overrightarrow {AC} \).
Cho hình lập phương \(ABCD.A'B'C'D'\) có độ dài các cạnh bằng a. Tính các tích vô hướng sau theo a:
a) \(\overrightarrow {AC} \cdot \overrightarrow {B'D'} \)
b) \(\overrightarrow {BD} \cdot \overrightarrow {B'C'} \)
c) \(\overrightarrow {A'B'} \cdot \overrightarrow {AC'} \)
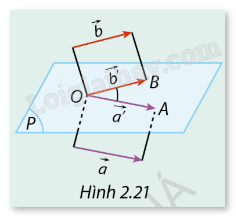
Trong không gian, cho hai vectơ \(\vec a,\vec b\) khác \(\vec 0\). Từ một điểm \(O\) tuỳ ý trong không gian, vẽ các vectơ \(\overrightarrow {{a^\prime }} ,\overrightarrow {{b^\prime }} \) sao cho \(\overrightarrow {{a^\prime }} = \vec a\), \(\overrightarrow {{b^\prime }} = \vec b\). (P) là mặt phẳng chứa giá của hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) (Hình 2.21).
a) Trong mặt phẳng \((P)\), hãy viết biểu thức tính \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \).
b) Hãy so sánh \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \) với \(|\vec a| \cdot |\vec b| \cdot \cos (\vec a,\vec b)\).
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính:
a) \(\overrightarrow {BC} .\overrightarrow {AH} ;\)
b) \(\overrightarrow {AF} .\overrightarrow {EG} ;\)
c) \(\overrightarrow {AC} .\overrightarrow {FE} .\)
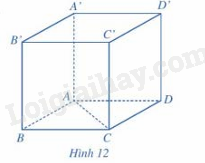
Trong không gian, cho hình lập phương ABCD.A’B’C’D’ có độ dài bằng 3cm (hình 12).
a, Tính góc giữa hai vecto \(\overrightarrow {AC} ,\overrightarrow {A'D'} \)
b, Tính \(\left| {\overrightarrow {AC} } \right|,\left| {\overrightarrow {A'D'} } \right|\). Cos(\(\overrightarrow {AC} ,\overrightarrow {A'D'} \))
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và tam giác \(ABC\) vuông cân tại \(B\), biết \(SA = AB = BC = a\). Gọi \(M\) là trung điểm của cạnh \(AC\). Tích vô hướng \(\overrightarrow {SM} \cdot \overrightarrow {BC} \)bằng
A. \(\frac{{{a^2}}}{2}\).
B. \({a^2}\).
C. \( - {a^2}\).
D. \( - \frac{{{a^2}}}{2}\).
Cho hình lập phương ABCD.A’B’C’D’ có độ dài cạnh là a. Khi đó, \(\overrightarrow {AB} .\overrightarrow {AD} \) bằng
