Có bao nhiêu cặp số \(x;y\) sao cho \(\left| x \right| + \left| y \right| = 4\)?
-
A.
$14$
-
B.
$16$
-
C.
$15$
-
D.
$18$
+ Tìm các số nguyên dương có tổng bằng \(4\) rồi lập bảng giá trị của \(\left| x \right|\) và \(\left| y \right|.\)
+ Từ đó suy ra các giá trị của \(x\) và \(y.\)
Vì \(x;y \in Z\) nên \(\left| x \right| \in N;\,\left| y \right| \in N\) mà \(\left| x \right| + \left| y \right| = 4\) nên ta có bảng
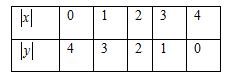
Suy ra
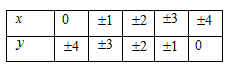
Với \(x = 0\) thì \(y = \pm 4\) nên gồm hai cặp số
Với \(x = 1\) thì \(y = \pm 2\) nên gồm hai cặp số
Với \(x = - 1\) thì \(y = \pm 2\) nên gồm hai cặp số
…
Với \(x = \pm 4\) thì \(y = 0\) nên gồm hai cặp số
Vậy có tất cả \(2.8 = 16\) cặp số nguyên \(\left( {x;y} \right)\) thỏa mãn \(\left| x \right| + \left| y \right| = 4.\)
Đáp án : B







