Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại \(A\), góc giữa A'C với mặt đáy \(\left( {ABC} \right)\) bằng \(45^\circ \) và \(AA' = 4\). Gọi \(M\) là trung điểm của CC'. Khoảng cách từ \(M\) đến mặt phẳng \(\left( {A'BC} \right)\) bằng

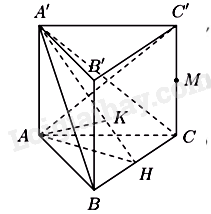
Gọi \(H\) là trung điểm của BC

Vì \(\Delta ABC\) vuông cân tại \(A\) nên \(AH \bot BC\)

Mà \(AA' \bot BC \Rightarrow \left( {A'AH} \right) \bot BC \Rightarrow \left( {A'AH} \right) \bot \left( {A'BC} \right)\)

Kẻ \(AK \bot A'H{\mkern 1mu} {\mkern 1mu} \left( {K \in A'H} \right)\)

Khi đó \(AK \bot \left( {A'BC} \right) \Rightarrow d\left( {A,\left( {A'BC} \right)} \right) = AK\)

Ta có: \(\left( {A'C,\left( {ABC} \right)} \right) = \left( {A'C,AC} \right) = \widehat {A'CA}\)

Theo giả thiết \(\angle A'CA = 45^\circ  \Rightarrow \widehat {A'AC}\) vuông cân tại \(A\)

Do đó \(AC = AA' = 4\)

Khi đó \(BC = AC\sqrt 2 {\rm{ \;}} = 4\sqrt 2 {\rm{ \;}} \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{4.4}}{{4\sqrt 2 }} = 2\sqrt 2 \)

Xét \(\Delta A'AH\) có \(AK \bot A'H\): \(AK = {\rm{ }}\frac{{AA'.AH}}{{\sqrt {AA{'^2} + A{H^2}} }} = \frac{{4.2\sqrt 2 }}{{\sqrt {16 + 8} }} = \frac{{4\sqrt 3 }}{3}\)

\( \Rightarrow d\left( {M,\left( {A'BC} \right)} \right) = \frac{1}{2}d\left( {A,\left( {A'BC} \right)} \right) = \frac{1}{2}.\frac{{4\sqrt 3 }}{3} = \frac{{2\sqrt 3 }}{3}\)

Vậy khoảng cách từ \(M\) đến mặt phẳng \(\left( {A'BC} \right)\)  bằng \(\frac{{2\sqrt 3 }}{3}\)

Đáp án A.