Đề bài
Cho khối lăng trụ tam giác đều ABC.A'B'C' có độ dài cạnh đáy bằng \(a\) và đường thẳng A'B hợp với mặt đáy một góc \(60^\circ \). Tính thể tích \(V\) của khối lăng trụ ABC.A'B'C'.
-
A.
\(V = \frac{{\sqrt 3 {a^3}}}{4}\).
-
B.
\(V = \sqrt 3 {a^3}\).
-
C.
\(V = \frac{{3{a^3}}}{4}\).
-
D.
\(V = \frac{{{a^3}}}{4}\).
Phương pháp giải
Thể tích của khối lăng trụ có diện tích đáy \(B\), chiều cao \(h\) là \(V = h.B\)
Lời giải của GV Loigiaihay.com
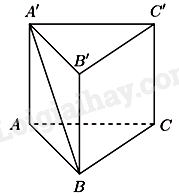
Ta có: \(AA' \bot \left( {ABC} \right) \Rightarrow \left( {A'B,\left( {ABC} \right)} \right) = \left( {A'B,AB} \right) = \widehat {A'BA}\)
Theo giả thiết \(\widehat {A'BA} = 60^\circ \)
Lại có: \(\tan 60^\circ = \frac{{AA'}}{{AB}} \Rightarrow AA' = AB\tan 60^\circ = a\sqrt 3 \)
Thể tích khối lăng trụ đã cho là \({V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = a\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4} = \frac{{3{a^3}}}{4}\)
Đáp án C.
Đáp án : C
