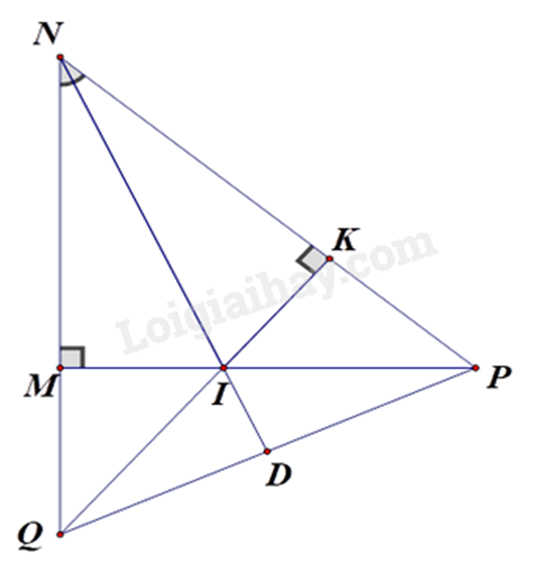
Cho \(\Delta MNP\) vuông tại M có MN < MP, kẻ đường phân giác NI của góc MNP (I thuộc MP). Kẻ IK vuông góc với NP tại K.
a) Chứng minh \(\Delta IMN = \Delta IKN\)
b) Chứng minh \({\rm{MI }} < {\rm{ IP}}\).
c) Gọi Q là giao điểm của đường thẳng IK và đường thẳng MN, đường thẳng \(NI\)cắt QP tại D. Chứng minh \(ND \bot QP\) và \(\Delta QIP\) cân tại I.
a) Chứng minh \(\Delta IMN = \Delta IKN\)(cạnh huyền - góc nhọn)
b) Chứng minh \(IM = IK\), IP > IK nên IP > IM.
c) Chứng minh I là trực tâm của tam giác QNP nên \(ND \bot QP\).
Chứng minh \(\Delta NQP\) cân tại \(N\) nên DQ = DP.
\(\Delta QIP\) có \(ID\) vừa là đường cao, vừa là đường trung tuyến nên \(\Delta QIP\) cân tại \(I\)
a) Xét \(\Delta IMN\) và \(\Delta IKN\) có:
\(\widehat {IMN} = \widehat {IKN} = {90^0}\)
NI chung
\(\widehat {MNI} = \widehat {KNI}\) (NI là đường phân giác NI của góc MNP)
suy ra \(\Delta IMN = \Delta IKN\)(cạnh huyền - góc nhọn) (đpcm)
b) Vì \(\Delta IMN = \Delta IKN\) nên IM = IK (hai cạnh tương ứng) (1)
Vì \(\Delta IKP\) vuông tại K nên IP > IK (2)
Từ (1) và (2) suy ra IP > IM (đpcm)
c) Xét \(\Delta NQP\) có đường cao QK và PM cắt nhau tại I nên I là trực tâm của tam giác NQP.
Do đó \(ND \bot QP\) (đpcm)
Vì \(\Delta NQP\) có ND vừa là đường cao vừa là đường phân giác nên \(\Delta NQP\) cân tại N.
Suy ra ND là đường trung tuyến của tam giác NQP hay QD = DP.
Xét \(\Delta QIP\) có ID vừa là đường cao vừa là đường trung tuyến nên \(\Delta QIP\) cân tại I.
Các bài tập cùng chuyên đề
Với \(a,b,c,d \in Z;\,\,b,d \ne 0;{\rm{b}} \ne \pm {\rm{d }}\). Kết luận nào sau đây là đúng?
Cho 3.4 = 6.2. Khẳng định nào sau đây đúng?
Có bao nhiêu đơn thức trong các biểu thức sau: \(2x\);\(8 + 4x\); \(5{x^6}\); \(5xy\); \(\frac{1}{{3x - 1}}\)?
Bậc của đa thức \(3{x^3} - 5{x^2} + 17x - 29\) là
Đa thức nào là đa thức một biến?
Tích của hai đơn thức \(7{x^2}\) và \(3x\) là
Một hộp phấn màu có nhiều màu: màu cam, màu vàng, màu đỏ, màu hồng, màu xanh. Hỏi nếu rút bất kỳ một cây bút màu thì có thể xảy ra mấy kết quả?
Bạn Lan gieo một con xúc xắc 8 lần liên tiếp thì thấy mặt \(4\) chấm xuất hiện \(3\) lần. Xác suất xuất hiện mặt \(4\) chấm là
Cho hình vẽ bên, với \(G\) là trọng tâm của \(\Delta ABC.\) Tỉ số của \(GD\) và \(AD\) là
Cho hình vẽ, chọn câu đúng?
Hình hộp chữ nhật có ba kích thước lần lượt là \(2a\);\(3a\); \(\frac{a}{3}\) . Thể tích của hình hộp chữ nhật đó là
Trong các hình sau, đâu là hình lăng trụ đứng tam giác?
Để ủng hộ các bạn vùng bão lũ Miền Trung học sinh ba lớp 7A, 7B, 7C của trường THCS A tham gia ủng hộ vở viết. Biết rằng số vở viết ủng hộ được của mỗi lớp lần lượt tỉ lệ với các số 2; 3; 4 và tổng số vở viết ủng hộ được của ba lớp là 360. Hỏi mỗi lớp ủng hộ được bao nhiêu quyển vở?
Cho \(A\left( x \right) = 4{x^2} + 4x + 1\).
a) Xác định bậc, hạng tử tự do, hạng tử cao nhất của đa thức.
b) Tìm B(x) biết \(A\left( x \right) + B\left( x \right) = 5{x^2} + 5x + 1\).
c) Tính \(A\left( x \right):\left( {2x + 1} \right)\).
Cho đa thức A (x) = \({x^2} + 2x + 2\). Chứng minh đa thức không có nghiệm.
