Đề bài
Cho ΔABC có: \(\widehat A = 3{5^0}\). Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của \(\widehat {ACB} \). Số đo các góc \(\widehat {ABC}; \widehat {ACB} \)là:
-
A.
\(\widehat {ABC} = 7{2^0}; \widehat {ACB} = 7{3^0}\)
-
B.
\(\widehat {ABC} = 7{3^0}; \widehat {ACB} = 7{2^0}\)
-
C.
\(\widehat {ABC} = 7{5^0}; \widehat {ACB} = 7{0^0}\)
-
D.
\(\widehat {ABC} = 7{0^0}; \widehat {ACB} = 7{5^0}\)
Phương pháp giải
Dựa vào đặc điểm của đường trung trực.
Sử dụng định lí tổng ba góc của một tam giác bằng \({180^0}\)
Lời giải của GV Loigiaihay.com
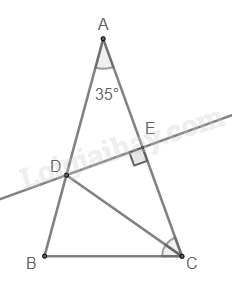
Đường trung trực của AC đi qua điểm D nên tam giác ADC cân tại D.
Do đó \(\widehat {DAC} = \widehat {DCA} = {35^0}\).
Mà CD là tia phân giác của \(\widehat {ACB}\) nên \(\widehat {ACB} = 2\widehat {DCA} = {2.35^0} = {70^0}\)
Từ đó suy ra:
\(\begin{array}{l}\widehat {ABC} = {180^0} - \widehat {BAC} - \widehat {BCA}\\ = {180^0} - {35^0} - {70^0} = {75^0}\end{array}\)
Vậy \(\widehat {ABC} = 7{5^0}; \widehat {ACB} = 7{0^0}\).
Đáp án C.
Đáp án : C
