Cho hình chóp tứ giác đều\(S.ABCD\)có tất cả các cạnh bằng \(a\). Tính khoảng cách từ đỉnh \(S\) đến mặt phẳng \((ABCD).\)

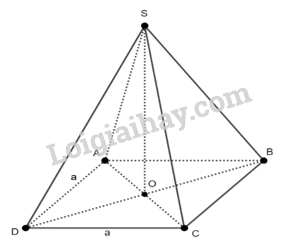
Gọi \(O\) là tâm của hình vuông \(ABCD.\) Suy ra \(SO \bot (ABCD)\) hay \(SO \bot BD\)

Xét hình vuông \(ABCD\) cạnh \(a,\) ta có \(AD = AB = a.\)

Suy ra \(BD = a\sqrt 2 \)(đường chéo hình vuông)\( \Rightarrow OD = \frac{{a\sqrt 2 }}{2}\)

Xét tam giác vuông \(SDO\)vuông tại \(O,\) áp dụng định lý Pitago ta có: \(S{D^2} = S{O^2} + O{D^2} \Rightarrow S{O^2} = S{D^2} - O{D^2} = {a^2} - {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} = \frac{{{a^2}}}{2} \Rightarrow SO = \frac{{a\sqrt 2 }}{2}\)

Vậy \(d(S,(ABCD)) = SO = \frac{{a\sqrt 2 }}{2}.\)