Cho tam giác \({\rm{ABC}},2\) trung tuyến \({\rm{BM}}\) và \({\rm{CN}}\) cắt nhau tại \({\rm{G}}\). Gọi \({\rm{D}},{\rm{E}}\) lần lượt là trung điểm \(GB\) và \(GC\). Chứng minh rằng:
a) \({\rm{MN}}//{\rm{DE}}\)
b) \({\rm{ND}}//{\rm{ME}}\)
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Tính chất: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
a) Chứng minh \(MN\parallel DE\) vì cùng song song với \({\rm{BC}}\)
b) Chứng minh được \({\rm{MN}} = {\rm{DE}}\) (sử dụng tính chất đường trung bình)
Chứng minh MNDE là hình bình hành suy ra điều phải chứng minh phần b.
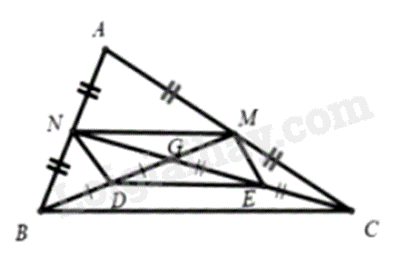
a) Vì \({\rm{BM}},{\rm{CN}}\) là 2 trung tuyến của \(\Delta ABC\left( {{\rm{GT}}} \right)\)
Suy ra \({\rm{M}},{\rm{N}}\) lần lượt là trung điểm của \({\rm{AB}},{\rm{AC}}\left( {{\rm{tc}}} \right)\)
Suy ra \({\rm{MN}}\) là đường trung bình \(\Delta ABC\) nên \({\rm{MN}}\parallel {\rm{BC}}\) (1)
Vì D, E lần lượt là trung điểm của GB, GC(GT) nên \({\rm{DE}}\) là đường trung bình của \(\Delta GBC\) nên \({\rm{DE}}\parallel {\rm{BC}}\) (2)
Từ (1) và \(\left( 2 \right) \Rightarrow MN\parallel DE\) (ĐL 3 đường thẳng song song)
b) Vì \({\rm{MN}}\) là đường trung bình \(\Delta ABC\) nên \({\rm{MN}} = \frac{{BC}}{2}\) (tc)
Vì \({\rm{DE}}\) là đường trung bình của \(\Delta GBC\) nên \({\rm{DE}} = \frac{{BC}}{2}\) (tc)
Suy ra \({\rm{MN}} = {\rm{DE}}\) mà \({\rm{MN}}\parallel {\rm{DE}}\) (theo \({\rm{a}}\))
Do đó MNDE là hình bình hành \(\left( {{\rm{DHNB}}} \right)\) suy ra \({\rm{ND}}\parallel {\rm{ME}}\left( {{\rm{tc}}} \right)\)
Các bài tập cùng chuyên đề
Đường trung bình của tam giác:
Hàm số nào dưới đây không phải hàm số bậc nhất?
Bác An đã gửi một lượng tiền tiết kiệm kì hạn 1 năm ở một ngân hàng với lãi suất 5,6%/năm (cứ sau kì hạn 1 năm, tiền lãi của kì hạn đó lại được cộng vào tiền vốn). Sau khi gửi 2 năm, bác An có được số tiền cả gốc và lãi là 111513600 đồng. Hỏi ban đầu bác An đã gửi vào ngân hàng số tiền là bao nhiêu đồng? Biết rằng lãi suất ngân hàng không thay đổi trong 2 năm đó.
Cho tam giác \(MNP\) có \(MD\) là tia phân giác của góc \(M\left( {D \in NP} \right)\). Trong các khẳng định sau, khẳng định nào đúng?
Cho các điểm \({\rm{A}}\left( { - 3;8} \right),{\rm{B}}\left( { - 2; - 5} \right),{\rm{C}}\left( {1;0} \right)\) và \({\rm{D}}\left( {\frac{1}{2};\frac{3}{4}} \right)\), điểm thuộc đồ thị của hàm số \(y = {x^2} - 1\) là:
Cho tam giác \({\rm{ABC}}\) Một đường thẳng \(d\) song song với \({\rm{BC}}\) và cắt các cạnh \({\rm{AB}},{\rm{AC}}\) của tam giác đó lần lượt tại \({\rm{M}},{\rm{N}}\) với \(\frac{{AM}}{{AB}} = \frac{1}{3}\) và \(AN + AC = 16{\rm{\;cm}}\). Tính \({\rm{AN}}\).
Để làm cây thông noel, người ta hàn một khung sắt có dạng hình tam giác cân \({\rm{ABC}}\left( {AB = AC = 2{\rm{\;m}}} \right)\) cùng các thanh sắt nằm ngang \({\rm{GF}},{\rm{HE}},{\rm{ID}},{\rm{BC}}\) và sau đó gắn cây thông như như hình vẽ. Tính số tiền sắt cần sử dụng để làm cây thông noel đó. Biết giá một mét sắt là 55000 đồng và \(AG = GH = HI = IB,CD = DE = EF = FA\), thanh \(GF\) dài \(0,2{\rm{\;m}}\).
Giải các phương trình sau:
a) \(0,1x - 5 = 0,2 - x\)
b) \(\frac{{2x - 5}}{3} = \frac{{2 - x}}{6}\);
c) \(\sqrt 3 x - 1 = x - 3\).
Cho ba đường thẳng \({d_1}:y = - 2x + 5;{d_2}:y = - 2x;{d_3}:y = 4x - 1\). Chỉ ra các cặp đường thẳng song song, cắt nhau hoặc trùng nhau.
Một tổ sản xuất của công ty may Đức Long được giao may một số áo sơ mi để xuất khẩu trong 20 ngày. Khi thực hiện, tổ sản xuất đó đã tăng năng suất \(20{\rm{\% }}\) nên sau 18 ngày không những đã xong số áo đó mà còn may thêm được 24 áo nữa. Tính số áo sơ mi mà tổ đó đã may được trên thực tế.
Cho hình vẽ, một người đứng ở vị trí \(M\) trên cây cầu bắc qua con kênh quan sát ba điểm thẳng hàng \({\rm{A}},{\rm{B}},{\rm{D}}\) lần lượt là chân hai cột đèn trồng ở bờ kênh và chân cầu. Người đó nhận thấy góc nhìn đến hai điểm \(A\), \({\rm{D}}\) thì bằng góc nhìn đến hai điểm \({\rm{B}},{\rm{D}}\), tức là \(\widehat {AMD} = \widehat {BMD}\). Người đó muốn ước lượng tỉ số khoảng cách từ vị trí \(M\) đang đứng đến điểm \(A\) và đến điểm \(B\) mà không cần phải đo trực tiếp hai khoảng cách đó. Hỏi có thể ước lượng tỉ số đó được hay không?
