Cho tam giác \({\rm{ABC}}\) có \(AB = 4,5{\rm{\;cm}},AC = 6{\rm{\;cm}}\). Các điểm \({\rm{M}},{\rm{N}}\) lần lượt thuộc các cạnh \({\rm{AB}},{\rm{AC}}\) thoả mãn \(AM = 3{\rm{\;cm}}\) và \(MN\parallel BC\). Tính độ dài đoạn thẳng \({\rm{AN}}\).
-
A.
\(3,5{\rm{\;cm}}\)
-
B.
\(5{\rm{\;cm}}\)
-
C.
\(4{\rm{\;cm}}\)
-
D.
\(6,5{\rm{\;cm}}\)
Định lí Thales trong \(\Delta {\rm{ABC}},{\rm{MN}}\parallel {\rm{BC}}\) ( \({\rm{M}}\) thuộc \({\rm{AB}},{\rm{N}}\) thuộc \({\rm{AC}}\) ): \(\frac{{{\rm{AM}}}}{{{\rm{AB}}}} = \frac{{{\rm{AN}}}}{{{\rm{AC}}}};\frac{{{\rm{AM}}}}{{{\rm{MB}}}} = \frac{{{\rm{AN}}}}{{{\rm{NC}}}};\frac{{{\rm{MB}}}}{{{\rm{AB}}}} = \frac{{{\rm{NC}}}}{{{\rm{AC}}}}\)
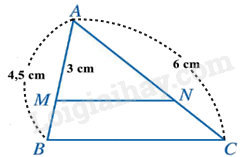
Xét tam giác \(ABC\) có \(MN\parallel BC\) nên: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (Định lí Thales)
Suy ra \(\frac{3}{{4,5}} = \frac{{AN}}{6}\) hay \(AN = 6.3:4,5 = 4{\rm{\;cm}}\)
Đáp án C.
Đáp án : C
