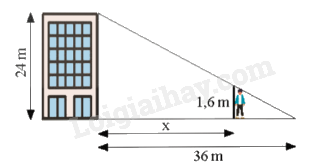
Một toà nhà cao \(24{\rm{\;m}}\), đổ bóng nắng dài \(36{\rm{\;m}}\) trên đường như hình sau. Một người cao 1,6 m muốn đứng trong bóng râm của toà nhà. Hỏi người đó có thể đứng cách toà nhà xa nhất bao nhiêu mét?
-
A.
\(36,3{\rm{\;m}}\)
-
B.
\(33,6{\rm{\;m}}\)
-
C.
\(36{\rm{\;m}}\)
-
D.
\(36,6{\rm{\;m}}\)
Dựng các điểm lên hình vẽ.
Áp dụng hệ quả định lí Thales: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ vơi ba cạnh của tam giác đã cho.
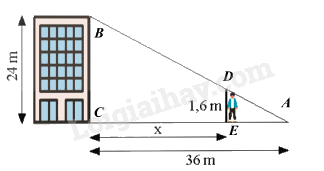
Xét \(\Delta ABC\) có \(DE//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{DE}}{{BC}} = \frac{{AE}}{{AC}} = \frac{{AC - CE}}{{AC}}\) hay \(\frac{{1,6}}{{24}} = \frac{{36 - x}}{{36}}\)
Suy ra \(36 - x = \frac{{1,6.36}}{{24}}\) hay \(x = 36 - \frac{{1,6.36}}{{24}} = 33,6\)
Vậy người đó có thể đứng xa tòa nhà nhất là \(33,6{\rm{\;m}}\).
Đáp án B.
Đáp án : B
