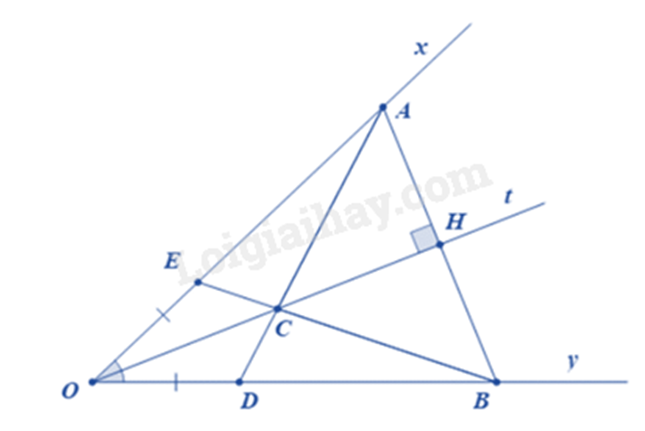
Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.
a) Chứng minh OA = OB.
b) Lấy điểm C nằm giữa O và H. Chứng minh \(\widehat {ACH} = \widehat {HCB}\).
c) AC cắt Oy ở D. Trên tia Ox lấy điểm E sao cho OE = OD. Chứng minh ba điểm B, C, E thẳng hàng.
a) Chứng minh được: ∆AHO = ∆BHO (góc – cạnh – góc)
Suy ra OA = OB (hai cạnh tương ứng)
b) Chứng minh được: ∆AHC = ∆BHC (hai cạnh góc vuông)
Suy ra \(\widehat {ACH} = \widehat {HCB}\) (hai góc tương ứng)
c) Chứng minh được: ∆OEC = ∆ODC (c.g.c)
Chứng minh được: \(\widehat {ECO} + \widehat {OCD} + \widehat {BCD} = {180^0}\)
Suy ra ba điểm E, C, B thẳng hàng.
a) Xét tam giác AHO và tam giác BHO có:
\(\widehat {AOH} = \widehat {BOH}\) (Ot là tia phân giác của \(\widehat {AOB}\))
OH chung
\(\widehat {AHO} = \widehat {BHO}\left( { = {{90}^0}} \right)\)
Suy ra \(\Delta AHO = \Delta BHO\left( {g.c.g} \right)\)
Suy ra OA = OB (hai cạnh tương ứng) (đpcm)
b) \(\Delta AHO = \Delta BHO\) suy ra AH = HB (hai cạnh tương ứng)
Xét tam giác AHC và tam giác BHC có:
HC chung
\(\widehat {AHC} = \widehat {BHC}\left( { = {{90}^0}} \right)\)
AH = HB
Suy ra \(\Delta AHC = \Delta BHC\) (hai cạnh góc vuông)
Suy ra \(\widehat {ACH} = \widehat {HCB}\) (hai góc tương ứng)
c) Xét tam giác OCE và OCD có:
OE = OD
\(\widehat {EOC} = \widehat {DOC}\)
OC chung
Suy ra ∆OEC = ∆ODC (c.g.c)
Suy ra EC = DC (hai cạnh tương ứng)
Ta có OA = OB và OE = OD nên AE = BD.
Xét \(\Delta ECA\) và \(\Delta DCB\) có:
EC = ED (cmt)
EA = DB (cmt)
CA = CB (\(\Delta AHC = \Delta BHC\))
Suy ra \(\Delta ECA = \Delta DCB\) (c.c.c)
Suy ra \(\widehat {ECA} = \widehat {DCB}\) (hai góc tương ứng)
Mặt khác \(\widehat {ECA} + \widehat {ECD} = {180^0}\) (vì AC cắt Oy tại D)
Suy ra \(\widehat {DCB} + \widehat {ECD} = {180^0}\) hay B, C, E thẳng hàng (đpcm).
Các bài tập cùng chuyên đề
Thay tỉ số 1,2 : 1,35 bằng tỉ số giữa các số nguyên ta được:
Biết \(\frac{x}{2} = \frac{y}{3}\) và \(x + y = - 15\). Khi đó giá trị của x, y là
Biết đại lượng y tỉ lệ thuận với đại lượng x với các cặp giá trị tương ứng trong bảng sau:
Giá trị cần điền vào “?” là
Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ a và khi \(x = - 2\) thì \(y = 4\). Khi đó, hệ số a bằng bao nhiêu?
Bộ ba độ dài đoạn thẳng nào sau đây tạo thành một tam giác?
Biểu thức đại số biểu thị tích của hai số tự nhiên liên tiếp là:
Trong các biểu thức sau, em hãy chỉ ra biểu thức số.
Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng
Giá trị của biểu thức \(A = 2{x^2} - 3x + 1\) tại \(x = - 1\) là
Tìm số hữu tỉ x trong các tỉ lệ thức sau:
a) \(\frac{{ - 6}}{x} = \frac{9}{{ - 15}}\)
b) \(\frac{{ - 4}}{x} = \frac{x}{{ - 49}}\)
a) Cho \(\frac{a}{b} = \frac{6}{5}\). Tìm a, b biết: a – b = 3
b) Cho \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\). Tìm x, y, z biết \(x - y + z = 32\)
Ba đơn vị cùng vận chuyển 700 tấn hàng. Đơn vị A có 10 xe trọng tải mỗi xe là 5 tấn; đơn vị B có 20 xe trọng tải mỗi xe là 4 tấn; đơn vị C có 14 xe trọng tải mỗi xe là 5 tấn. Hỏi mỗi đơn vị vận chuyển được bao nhiêu tấn hàng, biết mỗi xe đều chở một số chuyến như nhau?
Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Chứng minh: \(\frac{{ab}}{{cd}} = \frac{{{a^2} - {b^2}}}{{{c^2} - {d^2}}}\).
