Đề bài
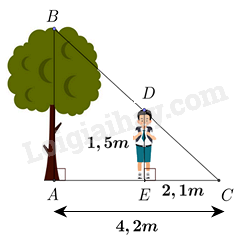
Một người cao 1,5 mét có bóng trên mặt đất dài 2,1 mét. Cùng lúc ấy, một cái cây gần đó có bóng trên mặt đất dài 4,2 mét. Tính chiều cao của cây.
-
A.
\(AB = 3m\).
-
B.
\(AB = 0,75m\).
-
C.
\(AB = 2,4m\).
-
D.
\(AB = 2,25m\).
Phương pháp giải
Dựa vào hệ quả của định lí Thales trong tam giác.
Lời giải của GV Loigiaihay.com
Vì cái cây và người đều vuông góc với mặt đất nên AB // DE.
Áp dụng hệ quả của định lí Thales vào tam giác ABC có DE // AB, ta có:
\(\frac{{CE}}{{AC}} = \frac{{DE}}{{AB}}\)
\(\frac{{2,1}}{{4,2}} = \frac{{1,5}}{{AB}} \Rightarrow AB = 1,5:\frac{{2,1}}{{4,2}} = 3\left( m \right)\)
Đáp án : A
