Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 2{\cos ^2}x + 5\sin x + 1\) trên \(\left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\).
Sử dụng kiến thức công thức: \({\cos ^2}x + {\sin ^2}x = 1\)
Ta có: \(y = 2{\cos ^2}x + 5\sin x + 1 = 2\left( {1 - {{\sin }^2}x} \right) + 5\sin x + 1 = - 2{\sin ^2}x + 5\sin x + 3\) (1)
Đặt \(\sin x = t\). Vì \(x \in \left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\) nên \(t \in \left[ {\frac{1}{2};1} \right]\).
Thay \(\sin x = t\) vào (1) ta có: \(y = - 2{t^2} + 5t + 3\) với \(t \in \left[ {\frac{1}{2};1} \right]\)
Ta có bảng:
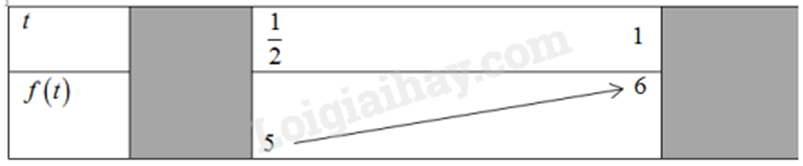
Từ bảng ta có:
Giá trị lớn nhất của hàm số đã cho trên \(\left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\) là 6 khi \(t = 1\) hay \(x = \frac{\pi }{2}\)
Giá trị nhỏ nhất của hàm số đã cho trên \(\left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\) là 5 khi \(t = \frac{1}{2}\) hay \(x = \frac{{5\pi }}{6}\)
Các bài tập cùng chuyên đề
Xét góc lượng giác \(\left( {OA,OM} \right) = \alpha \), trong đó M là điểm không nằm trên các trục tọa độ Ox và Oy. Khi đó, M thuộc góc phần tư nào để \(\sin \alpha \) và \(\cos \alpha \) trái dấu?
Cho \({90^0} < \alpha < {180^0}\). Chọn khẳng định đúng:
Trong các giá trị sau, \(\sin \alpha \) không thể nhận giá trị nào?
Chọn phát biểu đúng:
Tập xác định của hàm số \(y = 2\sin x\) là:
Chọn khẳng định đúng:
Dãy số \(\left( {{u_n}} \right)\) gồm các số nguyên dương chia hết cho 5. Số nào dưới đây thuộc dãy số \(\left( {{u_n}} \right)\)?
Cấp số cộng nào dưới đây có công sai bằng 3?
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 2\). Tính \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right)\)
Phát biểu nào sau đây là sai?
Giả sử hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục tại điểm \({x_o}\). Hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại điểm \({x_o}\) nếu:
Giá trị của \(\mathop {\lim }\limits_{x \to + \infty } {x^5}\) là:
Một mặt phẳng được xác định nếu mặt phẳng đó chứa:
Cho hình chóp S. ABCD với ABCD là hình bình hành. Hai điểm S và B cùng thuộc hai mặt phẳng:
Trong các mệnh đề sau, mệnh đề nào đúng?
Cho hình hộp ABCD. A’B’C’D’. Hình hộp đó có bao nhiêu mặt bên?
Khẳng định nào sau đây là sai?
Qua phép chiếu song song, tính chất nào không được bảo toàn?
Biết rằng \(\tan \alpha = 2\). Giá trị biểu thức \(\frac{{\sin \alpha + 2\cos \alpha }}{{3\sin \alpha - \cos \alpha }}\) \(\left( {\cos \alpha \ne 0} \right)\)là:
Cho tam giác ABC. Chọn đáp án đúng:
