Cho tứ giác ABCD có \(AB = CD\). Gọi M là trung điểm của BC. Gọi (P) là mặt phẳng đi qua M song song với AB và CD. Thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là hình gì?
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
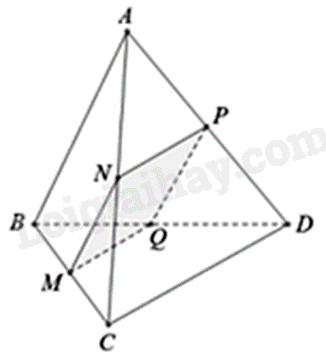
Vì (P) qua M và song song với AB nên \(\left( P \right) \cap \left( {ABC} \right) = MN\), với N là giao điểm của đường thẳng qua M song song với AB và cạnh AC.
Vì (P) qua N và song song với CD nên \(\left( P \right) \cap \left( {ACD} \right) = NP\), với P là giao điểm của đường thẳng qua N song song với CD và cạnh AD.
Vì (P) qua M và song song với CD nên \(\left( P \right) \cap \left( {BCD} \right) = MQ\), với Q là giao điểm của đường thẳng qua M song song với CD và cạnh BD.
Do đó, thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là tứ giác MNPQ.
Ta có: MN//PQ, \(MN = PQ = \frac{1}{2}AB\), MQ//PN, \(MQ = PN = \frac{1}{2}DC\), \(AB = CD\)
Do đó, \(MN = NP = PQ = QM\) nên tứ giác MNPQ là hình thoi.
Các bài tập cùng chuyên đề
Xét góc lượng giác \(\left( {OA,OM} \right) = \alpha \), trong đó M là điểm không nằm trên các trục tọa độ Ox và Oy. Khi đó, M thuộc góc phần tư nào để \(\sin \alpha \) và \(\cos \alpha \) trái dấu?
Cho \({90^0} < \alpha < {180^0}\). Chọn khẳng định đúng:
Trong các giá trị sau, \(\sin \alpha \) không thể nhận giá trị nào?
Chọn phát biểu đúng:
Tập xác định của hàm số \(y = 2\sin x\) là:
Chọn khẳng định đúng:
Dãy số \(\left( {{u_n}} \right)\) gồm các số nguyên dương chia hết cho 5. Số nào dưới đây thuộc dãy số \(\left( {{u_n}} \right)\)?
Cấp số cộng nào dưới đây có công sai bằng 3?
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 2\). Tính \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 6} \right)\)
Phát biểu nào sau đây là sai?
Giả sử hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục tại điểm \({x_o}\). Hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại điểm \({x_o}\) nếu:
Giá trị của \(\mathop {\lim }\limits_{x \to + \infty } {x^5}\) là:
Một mặt phẳng được xác định nếu mặt phẳng đó chứa:
Cho hình chóp S. ABCD với ABCD là hình bình hành. Hai điểm S và B cùng thuộc hai mặt phẳng:
Trong các mệnh đề sau, mệnh đề nào đúng?
Cho hình hộp ABCD. A’B’C’D’. Hình hộp đó có bao nhiêu mặt bên?
Khẳng định nào sau đây là sai?
Qua phép chiếu song song, tính chất nào không được bảo toàn?
Biết rằng \(\tan \alpha = 2\). Giá trị biểu thức \(\frac{{\sin \alpha + 2\cos \alpha }}{{3\sin \alpha - \cos \alpha }}\) \(\left( {\cos \alpha \ne 0} \right)\)là:
Cho tam giác ABC. Chọn đáp án đúng:
