Một con lắc lò xo treo thẳng đứng dao động điều hòa. Chu kỳ và biên độ dao động của con lắc lần lượt là 0,4 và 4\(\sqrt 2 \) cm. Lấy gia tốc trọng trường g =10 m/s² và  π² = 10 . Thời gian ngắn nhất từ khi lực đàn hồi của lò xo có độ lớn cực đại đến khi lực đàn hồi có độ lớn cực tiểu là

Từ T = 0,4s ta tìm được độ dãn ban đầu của lò xo.

Tần số góc:  

\(\omega  = \frac{{2\pi }}{T} = \sqrt {\frac{g}{{\Delta {l_0}}}}  \Rightarrow \frac{{2\pi }}{{0,4}} = \sqrt {\frac{g}{{\Delta {l_0}}}}  \Rightarrow \Delta {l_0} = 0,04m = 4cm\)

Độ dãn cực đại của lò xo là (A + ∆l₀) ứng với biên dương, khi đó lực đàn hồi cực đại. (Đáp án trục Ox hướng xuống dưới)

Khi lò xo ở vị trí không dãn thì lực đàn hồi cực tiểu và bằng 0. Sử dụng giản đồ vecto tìm thời gian vật đi từ biên dương đến bị trí - ∆l₀

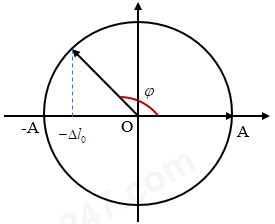
Ta có : \(\varphi  = \frac{\pi }{2} + \arccos \frac{{\Delta {l_0}}}{A} = \frac{\pi }{2} + \frac{\pi }{4} = \frac{{3\pi }}{4}\)

Thời gian : \(t = \frac{\varphi }{{2\pi }}.T = \frac{{\frac{{3\pi }}{4}}}{{2\pi }}.0,4 = 0,15s\)

Đáp án B.