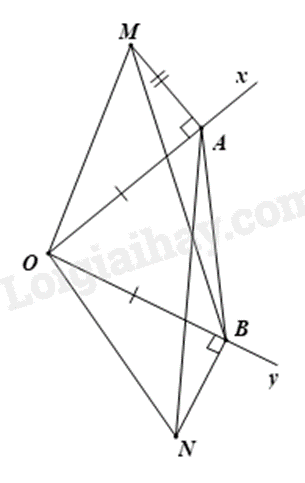
Cho \(\widehat {xOy}\) nhọn. Trên \(Ox\) lấy điểm \(A\) và trên \(Oy\) lấy điểm \(B\) sao cho \(OA = OB\). Vẽ ra phía ngoài \(\widehat {xOy}\) hai đoạn \(AM = BN\) sao cho \(AM \bot Ox\) và \(BN \bot Oy\). Chứng minh:
a. \(\Delta OMA = \Delta ONB\).
b. \(\widehat {AON\,}\)= \(\widehat {BOM}\) và \(\widehat {OMB}\)=\(\widehat {ONA}\).
a. \(\Delta OMA = \Delta ONB\left( {c - g - c} \right)\)
b. Theo a suy ra \(\widehat {AOM}\)=\(\widehat {BON}\)
Suy ra \(\widehat {AOM}\)+\(\widehat {AOB}\)=\(\widehat {AOB}\)+\(\widehat {BON}\)
Suy ra \(\widehat {AON\,}\)=\(\widehat {BOM}\)
Chứng minh \(\Delta OMB = \Delta ONA\left( {c - g - c} \right)\)
Suy ra \(\widehat {OMB}\)=\(\widehat {ONA}\)
a. \(\Delta OMA = \Delta ONB\left( {c - g - c} \right)\)
b. Theo a suy ra \(\widehat {AOM}\)=\(\widehat {BON}\)
Suy ra \(\widehat {AOM}\)+\(\widehat {AOB}\)=\(\widehat {AOB}\)+\(\widehat {BON}\)
Suy ra \(\widehat {AON\,}\)=\(\widehat {BOM}\)
Chứng minh \(\Delta OMB = \Delta ONA\left( {c - g - c} \right)\)
Suy ra \(\widehat {OMB}\)=\(\widehat {ONA}\)







