Đề bài
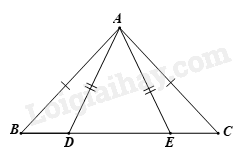
Cho hình vẽ sau có \(\widehat B = {48^O},\widehat {AED} = {65^O}\). Số đo \(\widehat {BAD}\) bằng
-
A.
\(20^\circ \).
-
B.
\(19^\circ \).
-
C.
\(18^\circ \).
-
D.
\(17^\circ \).
Phương pháp giải
Dựa vào tính chất tam giác cân, định lí tổng 3 góc trong một tam giác và tính chất của hai góc kề bù.
Lời giải của GV Loigiaihay.com
Xét tam giác ADE có \(AD = AE\) nên tam giác ADE cân tại A suy ra \(\widehat {ADE} = \widehat {AED} = {65^0}\).
Vì góc ADB và góc ADE là hai góc kề bù nên \(\widehat {ADB} + \widehat {ADE} = {180^0}\) suy ra \(\widehat {ADB} = {180^0} - {65^0} = {115^0}\).
Xét tam giác ABD, ta có:
\(\widehat {BAD} + \widehat {ADB} + \widehat B = {180^0}\) (tổng 3 góc trong một tam giác).
\( \Rightarrow \widehat {BAD} = {180^0} - \widehat B - \widehat {ADB} = {180^0} - {48^0} - {115^0} = {17^0}\).
Đáp án : D
