Hai đường chéo hình thoi có độ dài 8cm và 10cm. Cạnh của hình thoi có độ dài là:
-
A.
\(6cm\).
-
B.
\(\sqrt {41} cm\).
-
C.
\(\sqrt {164} cm\).
-
D.
\(9cm\).
Sử dụng định lí Pythagore để tính.
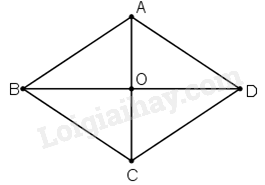
Xét hình thoi ABCD có AC = 8cm; BD = 10cm nên AO = 4 cm và OD = 5cm.
Áp dụng định lí Pythagore vào tam giác vuông OAD, ta có:
\(AD = \sqrt {O{A^2} + O{D^2}} = \sqrt {{4^2} + {5^2}} = \sqrt {41} \left( {cm} \right)\)
Đáp án : B
Các bài tập cùng chuyên đề
Cho hình chóp tam giác đều có độ dài cạnh bên bằng 4 cm và độ dài cạnh đáy bằng 3cm như hình bên dưới, hình nào là hình khai triển của hình chóp tam giác đều đã cho? 
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3cm, chiều cao của hình chóp là h = 2cm. Thể tích của hình chóp đã cho là :
Cho biểu thức : \(A = \frac{1}{{x + 4}} + \frac{x}{{x - 4}} + \frac{{24 - {x^2}}}{{{x^2} - 16}}\)
a) Viết điều kiện xác định của biểu thức A.
b) Chứng minh \(A = \frac{5}{{x - 4}}\).
c) Tính giá trị của biểu thức A tại x = 10.
d) Tìm các số nguyên x để giá trị của biểu thức A là số nguyên.
a) Rút gọn biểu thức sau:
\(A = \left( {x + 5} \right)\left( {x + 1} \right) + \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right) - x\left( {{x^2} + x - 2} \right)\)
b) Tính nhanh: 742 + 242 – 48.74.
1. Trên giấy kẻ ô vuông (độ dài ô vuông bằng 1cm ), cho tam giác ABC như hình bên. Tính độ dài mỗi cạnh của tam giác ABC 
2. Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC và K là điểm đối xứng với M qua điểm I.
a) Tứ giác AKCM là hình gì? Vì sao?
b) Chứng minh: AKMB là hình bình hành.
c) Tìm điều kiện của tam giác ABC để tứ giác AKCM là hình vuông.
