Cho hình chữ nhật ABCD có AB = 2AD. Vẽ BH vuông góc với AC . Gọi M, N, P lần lượt là trung điểm của AH, BH, CD.
a) Chứng minh tứ giác MNCP là hình bình hành.
b) Chứng minh MP vuông góc MB.
c) Gọi I là trung điểm của BP và J là giao điểm của MC và NP. Chứng minh rằng: MI – IJ < JP
a) Chứng minh tứ giác MNCP có hai cạnh đối song song và bằng nhau.
b) Chứng minh N là trực tâm của tam giác CMB nên NC\( \bot \)MB\( \Rightarrow \) MP\( \bot \)MB (MP // CN).
c) Chứng minh MI = PI, sử dụng bất đẳng thức tam giác để chứng minh PI – IJ < JP hay MI – IJ < JP.
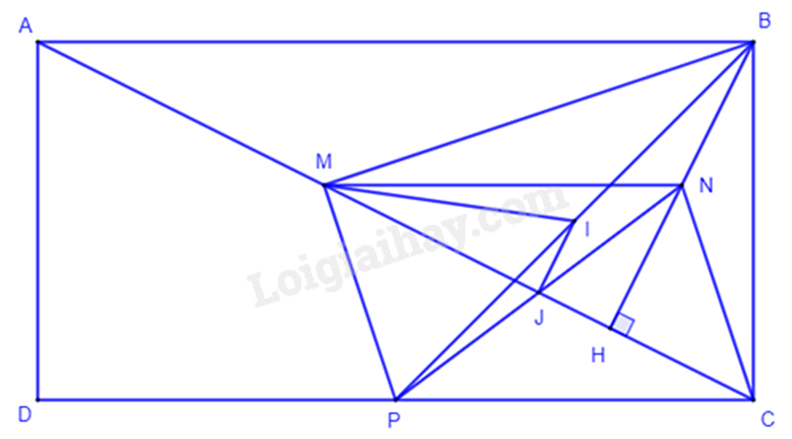
a) Xét tam giác AHB có:
M là trung điểm của AH
N là trung điểm của BH
Suy ra MN là đường trung bình của tam giác AHB. DO đó MN // AB và MN = \(\frac{1}{2}\)AB.
Vì P là trung điểm của CD nên CP = PD = \(\frac{1}{2}\)CD.
Mà AB // CD; AB = CD (ABCD là hình chữ nhật) nên CP = \(\frac{1}{2}\)AB.
Suy ra MN // CP (cùng song song với AB) và MN = CP (\(\frac{1}{2}\)AB).
Do đó tứ giác MNCP là hình bình hành (đpcm)
b) Do MN // AB (cmt) mà AB \( \bot \) BC (ABCD là hình chữ nhật) nên MN \( \bot \) BC.
Ta có BH \( \bot \) MC (gt)
Mà MN \( \cap \) BH tại N.
Suy ra N là trực tâm của tam giác CMB, do đó CN \( \bot \) BM.
Mà CN // PM (MNCP là hình bình hành)
Suy ra PM \( \bot \) BM (đpcm)
c) Xét tam giác PMB vuông tại M có I là trung điểm của BP nên MI là đường trung tuyến ứng với cạnh huyền của tam giác PMB suy ra MI = \(\frac{1}{2}\)BP = PI.
Xét tam giác PIJ, ta có: PI – IJ < JP hay MI – IJ < JP (đpcm).








Bình luận