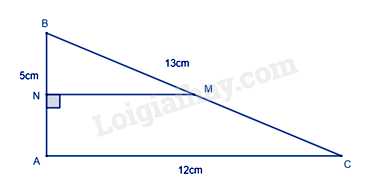
Cho tam giác ABC có AB = 5cm, AC = 12cm và BC = 13cm. Gọi M là trung điểm của BC. Từ M kẻ đường thẳng vuông góc với AB cắt AB tại N. Tính MN?
-
A.
4cm
-
B.
5cm
-
C.
6cm
-
D.
3cm
* Ta có: AB2 + AC2 = BC2 (52 + 122 = 132 = 169)
Suy ra: tam giác ABC vuông tại A
⇒ AB ⊥ AC
* Lại có: MN ⊥ AB nên MN // AC.
* Vì MN // AC và M là trung điểm của BC nên N là trung điểm của AB.
Khi đó, MN là đường trung bình của tam giác ABC .
\(MN = \frac{1}{2}AC = \frac{1}{2}.12 = 6cm\)
Đáp án : C
Các bài tập cùng chuyên đề
Chọn câu đúng.
Cho tam giác ABC có E, F lần lượt là trung điểm của AB, BC. Phát biểu nào sau đây là đúng:
Chọn câu đúng. Cho hình vẽ sau:
Đường trung bình của tam giác ABC là:
Cho các khẳng định dưới đây:
1) Trong một tam giác chỉ có một đường trung bình.
2) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
3) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng cạnh ấy.
Trong các khẳng định trên, số khẳng định đúng là
Cho tam giác MNP có A, B theo thứ tự là trung điểm của NP, MN. Biết AB = 3dm. Khi đó:
Cho tam giác ABC, gọi M, N và P lần lượt là trung điểm của AB, AC và BC. Hỏi có bao nhiêu hình thang trong hình vẽ ?
Cho tam giác ABC có BC = 6cm, các đường trung tuyến BE, CD. Khi đó độ dài cạnh DE là
Cho tam giác AMN như hình vẽ dưới đây. Biết AE = EM; AF = FN; EF = 9cm độ dài đoạn thẳng MN là
Hãy chọn câu đúng?
Cho ΔABC, I, K lần lượt là trung điểm của AB và AC. Biết BC = 8 cm, AC = 7cm. Ta có:
Cho hình vẽ dưới đây: Biết ME = EP, DN = 10cm; và DE // NP. Khi đó độ dài đoạn thẳng DM là
Cho tam giác ABC. Trên cạnh AB, AC lần lượt lấy các điểm E, F sao cho AE = BE, AF = FC. Khi đó \(\frac{{BC}}{{EF}}\) bằng:
Cho tam giác ABC vuông tại A như hình vẽ dưới đây: Biết AB = 6cm;
AC = 8 cm Độ dài đường trung bình ứng với cạnh BC là
Cho tam giác ABC có chu vi bằng 32cm. Gọi E, F, P là trung điểm của các cạnh AB, BC, AC. Chu vi của tam giác PFE bằng:
Cho hình vẽ dưới đây. Tìm x.
Cho tam giác đều ABC cạnh 12cm. Gọi M, N lần lượt là trung điểm của AB và AC. Chu vi tứ giác MNBC là:
Cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Biết BD = 18cm. Tổng độ dài hai đoạn thẳng HE và GF là:
Cho tam giác đều ABC có chu vi bằng 30cm. Độ dài đường trung bình ứng với cạnh AB là:
Cho hình dưới đây biết AD = DB, AE = EC, GM = MB; GN = NC, GI = IM; GK = KN; BC = 28cm. Khi đó tổng DE + IK bằng:
Cho tam giác ABC . Gọi D, E, F lần lượt là trung điểm của AB, AC, BC. Chu vi tam giác DEF là 21cm. Chu vi tam giác ABC là:
Cho tam giác ABC có AB = 24cm; AC = 36cm. Kẻ BD \(\left( {A \in AC} \right)\) góc với tia phân giác của góc A tại H. Gọi M là trung điểm của BC. Độ dài đoạn thẳng HM là:
