Gieo hai con xúc xắc. Có bao nhiêu kết quả thuận lợi cho biến cố “Số chấm xuất hiện trên hai con xúc xắc là số chẵn”.
-
A.
2.
-
B.
4.
-
C.
6.
-
D.
3.
Sử dụng lý thuyết kết quả thuận lợi: Một kết quả có thể của T để biến cố E xảy ra được gọi là kết quả thuận lợi cho biến cố E.
Các kết quả có thể là: mặt 1 chấm, mặt 2 chấm, mặt 3 chấm, mặt 4 chấm, mặt 5 chấm, mặt 6 chấm,
Kết quả thuận lợi cho biến cố “Số chấm xuất hiện trên hai con xúc xắc là số chẵn” là mặt 2 chấm, mặt 4 chấm, mặt 6 chấm. nên có 3 kết quả thuận lợi.
Đáp án : D

Các bài tập cùng chuyên đề
Có hai chiếc hộp: hộp thứ nhất chứa 3 bi xanh được đánh số từ 1 đến 3, hộp thứ hai chứa 3 bi đỏ được đánh số từ 1 đến 3 và 3 bi vàng được đánh số từ 1 đến 3. Lấy ngẫu nhiên mỗi hộp một viên bi. Tính số phần tử của biến cố A: “Ba bi được chọn vừa khác màu vừa khác số"
-
A.
3
-
B.
4
-
C.
5
-
D.
6
Trở lại tình huống mở đầu, kết quả của hành động rút ngẫu nhiên một phiếu câu hỏi của Sơn là một câu hỏi nào đó trong số 20 câu hỏi được đánh số từ 1 đến 20. Có 20 kết quả có thể là phiếu số 1, phiếu số 2,.., phiếu số 20.
Xét biến cố E: "Sơn rút được phiếu câu hỏi thuộc lĩnh vực Lịch sử - Địa lí"
Em hãy xác định các kết quả có thể để biến cố E xảy ra
Trở lại ví dụ 2, hãy liệt kê các kết quả thuận lợi cho các biến cố sau:
- G: "Chọn được một bạn nam";
- H: "Chọn được một bạn lớp 8C hoặc 8D"
Vuông thực nghiệm gieo một con xúc xắc
a) Liệt kê các kết quả có thể của thực nghiệm trên
b) Liệt kê các kết quả thuận lợi cho các biến cố sau:
- A: "Số chấm xuất hiện trên con xúc xắc là hợp số"
- B: "Số chấm xuất hiện trên con xúc xắc nhỏ hơn 5"
- C: "Số chấm xuất hiện trên con xúc xắc là số lẻ"
Một hộp đựng 12 tấm thẻ, được ghi số 1; 2;...; 12. Bạn Nam rút ngẫu nhiên một tấm thẻ trong hộp
a) Liệt kê các kết quả có thể của hành động trên
b) Liệt kê các kết quả thuận lợi cho các biến cố sau:
- A: "Rút được tấm thẻ ghi số chẵn"
- B: "Rút được tấm thẻ ghi số nguyên tố";
- C: "Rút được tấm thẻ ghi số chính phương"
Bạn An có 16 cuốn sách , trong đó có 4 cuốn sách tiểu thuyết , 5 cuốn sách lịch sử, 3 cuốn sách Khoa học tự nhiên và 4 cuốn sách Toán. Các cuốn sách này được xếp tùy ý trong tủ sách. Bạn Bình đến chơi là lấy ngẫu nhiên một cuốn sách trong tủ sách của An
a) Liệt kê các kết quả có thể của hành động trên
b) Liệt kê các kết quả thuận lợi cho các biến cố sau:
E: "Bình lấy được một cuốn sách tiểu thuyết"
F: "Bình lấy được một cuốn sách Khoa học tự nhiên hoặc cuốn sách Toán"
G: "Bình lấy được một cuốn sách không phải là sách Lịch sử"
Trong một hộp có 10 tấm thẻ giống nhau được đánh số 11; 12;...; 20. Rút ngẫu nhiên một tấm thẻ từ trong hộp
a) Liệt kê các kết quả có thể của hành động trên.
b) Liệt kê các kết quả thuận lợi cho biến cố sau:
E: "Rút được tấm thẻ ghi số là bội của 3"
F: "Rút được tấm thẻ ghi số nguyên tố"
Một hộp chứa 10 tấm thẻ cùng loại được đánh số lần lượt từ 3 đến 12. Chọn ngẫu nhiên 1 tấm thẻ từ hộp. Hãy liệt kê các kết quả làm cho các biến cố sau xảy ra.
\(A\):” Số ghi trên thẻ lấy ra chia hết cho 3”.
\(B\):” Số ghi trên thẻ lấy ra chia hết cho 6”.
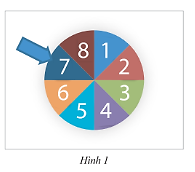
Trên bàn có một tấm bìa hình tròn được chia thành 8 phần hình quạt bằng nhau và được đánh số từ 1 đến 8 như Hình 1. Xoay tấm bìa quanh tâm hình tròn và xem khi tấm bìa dừng lại, mũi tên chỉ vào ô ghi số nào. Xét các biến cố sau:
\(A\): “Mũi tên chỉ vào ô ghi số chẵn”;
\(B\): “Mũi tên chỉ vào ô ghi số chia hết cho 4”;
\(C\): “Mũi tên chỉ vào ô ghi số nhỏ hơn 3”.
Hãy nêu các kết quả thuận lợi cho mỗi biến cố trên.
Trong túi có \(9\) viên bi có cùng kích thước và khối lượng, được đánh số từ \(1\) đến \(9,\) trong đó có \(2\) viên bi đỏ, \(3\) viên bi xanh và \(4\) viên bi vàng. Lấy ngẫu nhiên một viên bi trong túi. Khi đó:
a) Có bao nhiêu kết quả có thể xảy ra? Các kết quả đó có đồng khả năng hay không?
b) Xét các biến cố:
+ A: “Lấy được viên bi màu đỏ”;
+ B: “Lấy được viên bi màu xanh”;
+ C: “Lấy được viên bi màu vàng”.
Hãy tìm số thích hợp với mỗi câu sau:
- Có ? kết quả để biến cố A xảy ra;
- Có ? kết quả để biến cố B xảy ra;
- Có ? kết quả để biến cố C xảy ra.
Một hộp đựng 20 tấm thẻ được ghi số 1, 2, …, 20. Bạn Mai rút ngẫu nhiên một tấm thẻ từ trong hộp.
a) Liệt kê các kết quả có thể của hành động trên.
b) Liệt kê các kết quả thuận lợi cho các biến cố sau:
- E: “Rút được tấm thẻ ghi số lẻ”;
- F: “Rút được tấm thẻ ghi số chia hết cho 5”;
- G: “Rút được tấm thẻ ghi số nguyên tố”.
Một túi đựng 5 viên bi được ghi số 1, 2, 3, 4, 5. Bạn Bình lấy ngẫu nhiên hai viên bi từ trong hộp.
a) Liệt kê các kết quả có thể của hành động trên.
b) Liệt kê các kết quả thuận lợi cho các biến cố sau:
- M: “Tổng hai số ghi trên hai viên bi là một số chẵn”;
- N: “Tích hai số ghi trên hai viên bi là một số lẻ”.
Rút ngẫu nhiên một tấm thẻ từ một hộp chứa các tấm thẻ ghi số 1; 2; …; 30. Số kết quả thuận lợi cho biến cố “Rút được tấm thẻ ghi số chia hết cho 5” là
A. 5.
B. 6.
C. 7.
D. 4.
Một lớp học có 30 học sinh, trong đó có 12 học sinh nữ. Trong lớp có 2 học sinh nữ cận thị và 6 học sinh nam không cận thị. Chọn ngẫu nhiên một học sinh trong lớp. Số kết quả thuận lợi cho biến cố “Học sinh đó cận thị” là
A. 13.
B. 15.
C. 14.
D. 16.
Vuông thực nghiệm gieo một con xúc xắc.
a) Liệt kê các kết quả có thể của thực nghiệm trên.
b) Liệt kê các kết quả thuận lợi cho các biến cố sau:
- A: "Số chấm xuất hiện trên con xúc xắc là hợp số";
- B: "Số chấm xuất hiện trên con xúc xắc nhỏ hơn 5";
- C: "Số chấm xuất hiện trên con xúc xắc là số lẻ".
Một hộp đựng 12 tấm thẻ, được ghi số 1; 2;...; 12. Bạn Nam rút ngẫu nhiên một tấm thẻ trong hộp
a) Liệt kê các kết quả có thể của hành động trên.
b) Liệt kê các kết quả thuận lợi cho các biến cố sau:
- A: "Rút được tấm thẻ ghi số chẵn";
- B: "Rút được tấm thẻ ghi số nguyên tố";
- C: "Rút được tấm thẻ ghi số chính phương".
Lớp 8B có 16 học sinh nam, 22 học sinh nữ, trong đó có 13 học sinh nam thuận tay phải, kí hiệu là A1, A2,…, A3; 3 học ính nam thuận tay trái, kí hiệu là B1, B2, B3; 20 học sinh nữ thuận tay phải, kí hiệu là C1, C2,…, C20 và 2 học sinh nữ thuận tay trái, kí hiệu là D1, D2. Chọn ngẫu nhiên một học sinh trong lớp.
a) Liệt kê tất cả các kết quả có thể.
b) Liệt kê các kết quả thuận lợi cho biến cố E: “Học sinh đó là nam thuận tay phải”.
c) Liệt kê các kết quả thuận lợi cho biến cố F: “Học sinh đó thuận tay trái”.
Bạn An có 16 cuốn sách , trong đó có 4 cuốn sách tiểu thuyết , 5 cuốn sách lịch sử, 3 cuốn sách Khoa học tự nhiên và 4 cuốn sách Toán. Các cuốn sách này được xếp tùy ý trong tủ sách. Bạn Bình đến chơi là lấy ngẫu nhiên một cuốn sách trong tủ sách của An
a) Liệt kê các kết quả có thể của hành động trên
b) Liệt kê các kết quả thuận lợi cho các biến cố sau:
E: "Bình lấy được một cuốn sách tiểu thuyết"
F: "Bình lấy được một cuốn sách Khoa học tự nhiên hoặc cuốn sách Toán"
G: "Bình lấy được một cuốn sách không phải là sách Lịch sử"
Một túi đựng 5 viên bi, được ghi số 1, 2, 3, 4, 5. Bạn Bình lấy ngẫu nhiên hai viên bi từ trong tủ.
a) Liệt kê các kết quả có thể của hành động trên.
b) Liệt kê các kết quả thuận lợi cho các biến cố sau:
- M: “Tổng hai số ghi trên hai viên bi là một số chẵn”;
- N: “Tích hai số ghi trên hai viên bi là một số lẻ”.
Trong một hộp có 10 tấm thẻ giống nhau được đánh số 11; 12;...; 20. Rút ngẫu nhiên một tấm thẻ từ trong hộp
a) Liệt kê các kết quả có thể của hành động trên.
b) Liệt kê các kết quả thuận lợi cho biến cố sau:
E: "Rút được tấm thẻ ghi số là bội của 3"
F: "Rút được tấm thẻ ghi số nguyên tố"

Một hộp đựng 20 tấm thẻ cùng loại được đánh số thứ tự 1; 2; …; 20. Lấy ngẫu nhiên một thẻ từ hộp. Hãy nêu các kết quả thuận lợi cho mỗi biến cố sau:
A: “Số ghi trên thẻ lấy ra là bội của 5”;
B: “Số ghi trên thẻ lấy ra là ước của 24”.
Cho tấm bìa hình tròn như Hình 2. Xoay tấm bìa quanh tâm của nó và xem khi tấm bìa dừng lại, mũi tên chỉ vào ô ghi số nào.
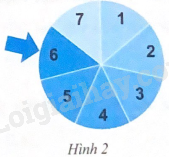
Hãy nêu các kết quả thuận lợi cho mỗi biến cố sau:
A: “Mũi tên chỉ vào ô ghi số lớn hơn 3”;
B: “Mũi tên chỉ vào ô ghi số lẻ”.
Một hộp đựng 5 thẻ, đánh số từ 1 đến 5. Chọn ngẫu nhiên 3 thẻ. Gọi A là biến cố để tổng số của 3 thẻ được chọn bằng 8. Số kết quả thuận lợi của biến cố A là:
-
A.
2
-
B.
3
-
C.
4
-
D.
5
Gieo đồng tiền hai lần. Có mấy kết quả thuận lợi cho biến cố “Mặt ngửa xuất hiện ít nhất 1 lần” là:
-
A.
2
-
B.
4
-
C.
3
-
D.
6
Từ các chữ số 1,2,3,4 ta lập các số tự nhiên có 3 chữ số khác nhau. Phát biểu biến cố A = {123,234,124,134} dưới dạng mệnh đề:
-
A.
Số tự nhiên có ba chữ số được thành lập từ các chữ số 1,2,3,4
-
B.
Số tự nhiên có ba chữ số được thành lập từ các chữ số 1, 2, 3, 4 có chữ số đứng sau lớn hơn chữ số đứng trước
-
C.
Số tự nhiên có ba chữ số được thành lập từ các chữ số 1, 2, 3, 4 chia hết cho 2 hoặc 3
-
D.
Số tự nhiên có ba chữ số được thành lập từ các chữ số 1, 2, 3, 4 có chữ số tận cùng là 3 hoặc 4.
Gieo một con xúc xắc, số chấm trên con xúc xắc là bao nhiêu để biến cố “số chấm xuất hiện là số nguyên tố” chắc chắn xảy ra?
-
A.
1; 2; 5
-
B.
2; 3; 5
-
C.
1; 4; 6
-
D.
2; 4; 5
Gieo ngẫu nhiên xúc xắc một lần. Liệt kê các kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chia 4 dư 1”.
-
A.
Có một kết quả thuận lợi cho biến cố là mặt 1 chấm.
-
B.
Có hai kết quả thuận lợi cho biến cố là mặt 1 chấm, mặt 5 chấm.
-
C.
Có ba kết quả thuận lợi cho biến cố là mặt 1 chấm, mặt 2 chấm, mặt 5 chấm.
-
D.
Không có kết quả thuận lợi nào.
Trong một trò chơi, Xuân được chọn làm người may mắn để rút thăm trúng thưởng. Gồm 4 loại thăm: hai hộp bút màu, hai bức tranh, một đôi giày và một cái bàn. Có bao nhiêu kết quả thuận lợi cho biến cố “Xuân chọn được phần thưởng là một hộp bút màu”, biết Xuân được rút duy nhất một lần.
-
A.
2
-
B.
4
-
C.
1
-
D.
3
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ. Nêu những kết quả thuận lợi cho biến cố “Số trên thẻ nhỏ hơn 4” .
-
A.
5
-
B.
1, 2, 3, 4, 5
-
C.
1, 2, 3
-
D.
1,2
Viết ngẫu nhiên một số tự nhiên có hai chữ số. Tìm số phần tử của tập hợp D gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra của biến cố sau “Số tự nhiên được viết ra là bình phương của một số tự nhiên”
-
A.
Có bốn kết quả thuận lợi cho biến cố là 25, 36, 49, 64.
-
B.
Có năm kết quả thuận lợi cho biến cố là 16, 25, 36, 49, 64.
-
C.
Có sáu kết quả thuận lợi cho biến cố là 16, 25, 36, 49, 64, 81.
-
D.
Có hai kết quả thuận lợi cho biến cố là 16, 25.







Danh sách bình luận