Trong hình vẽ bên dưới, các điểm A’, B’, C’, D’ lần lượt là trung điểm của các đoạn thẳng OA, OB, OC, OD.

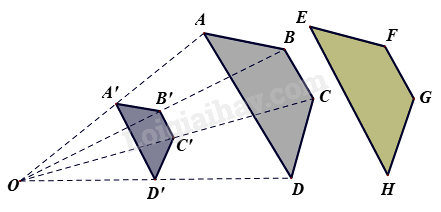
Cho các khẳng định sau:

+ Hình thang ABCD và EFGH bằng nhau

+ Hình thang A’B’C’D và hình thang EFGH đồng dạng với nhau

+ Hình thang ABCD đồng dạng phối cảnh với hình thang A’B’C’D’

Có bao nhiêu khẳng định đúng?

+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H₁ đồng dạng phối cảnh với hình H và bằng hình H’

+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H

- Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):

+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.

+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)