Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng a, cạnh bên bằng 2a. Gọi I, H lần lượt là trung điểm cạnh AB, CD. Tính thể tích V của khối chóp S.IBCH.
-
A.
\(V = \frac{{{a^3}\sqrt 2 }}{{12}}\).
-
B.
\(V = \frac{{{a^3}\sqrt 2 }}{6}\).
-
C.
\(V = \frac{{{a^3}\sqrt 2 }}{4}\).
-
D.
\(V = \frac{{{a^3}\sqrt 2 }}{8}\).
Sử dụng kiến thức về hình chóp đều, định lý Pythagore và diện tích tam giác đều để tính.
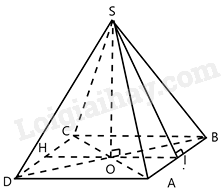
Tứ giác ABCD là hình vuông cạnh a nên diện tích ABCD bằng: \({S_{ABCD}} = {a^2}\)
Xét tam giác vuông ABC có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
Suy ra \(AO = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác vuông SOA có: \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{a^2} - {{(\frac{{a\sqrt 2 }}{2})}^2}} = \frac{{a\sqrt 2 }}{2}\)
\({V_{SABCD}} = \frac{1}{3}.{S_{ABCD}}.SO = \frac{1}{3}.{a^2}.\frac{{a\sqrt 2 }}{2} = \frac{1}{3}.{a^2}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 2 }}{6}\)
\(\frac{{{V_{SIBCH}}}}{{{V_{SABCD}}}} = \frac{{\frac{1}{3}.{S_{IBCH}}.h}}{{\frac{1}{3}.{S_{ABCD}}.h}} = \frac{{{S_{IBCH}}}}{{{S_{ABCD}}}} = \frac{{IB.BC}}{{AB.BC}} = \frac{{BI}}{{AB}} = \frac{1}{2}\)
Do đó \({V_{SIBCH}} = \frac{1}{2}{V_{SABCD}} = \frac{1}{2}.\frac{{{a^3}\sqrt 2 }}{6} = \frac{{{a^3}\sqrt 2 }}{{12}}\)
Đáp án : A

Các bài tập cùng chuyên đề
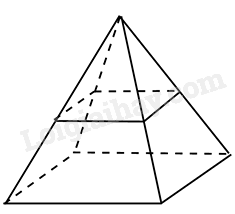
Người ta làm một bugalow dạng hình chóp tứ giác đều có chiều cao 4m, cạnh sàn nhà bằng 6m. Người ta chia đôi làm hai tầng bằng một mặt phẳng song song với sàn, cách đỉnh của hình chóp một khoảng bằng nửa chiều cao, cạnh mặt sàn tầng hai bằng một nửa cạnh mặt sàn tầng một. Biết một người cần \(3{m^3}\)không khí, tính số người tối đa ở tầng dưới. ( hình vẽ dưới)
-
A.
16 người.
-
B.
20 người.
-
C.
18 người.
-
D.
14 người.
Bạn Hùng có một cái gàu có dạng hình chóp tứ giác đều và một cái thùng (không chứa nước) có dạng hình lăng trụ đứng. Hai vật này có cùng diện tích đáy và chiều cao (Hình 3a). Hùng múc đầy một gày nước và đổ vào thùng thì thấy chiều cao của cột nước bằng \(\frac{1}{3}\) chiều cao của thùng (Hình 3b). Gọi \(S\)đáy là diện tích đáy và \(h\) là chiều cao của cái gàu.
a) Tính thể tích \(V\) của phần nước đổ vào theo S đáy và \(h\).
b) Từ câu a), hãy dự đoán thể tích của cái gàu.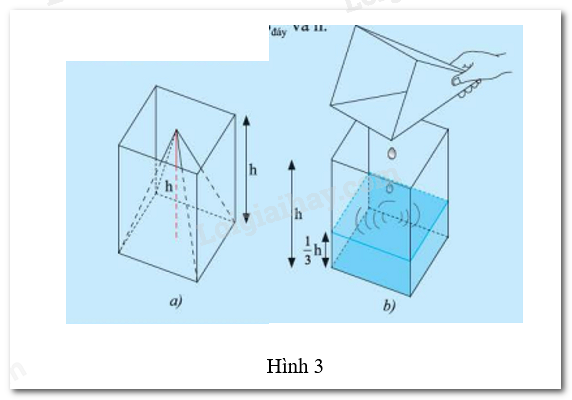
Tính thể tích của một chiếc hộp bánh ít có dạng hình chóp tứ giác đều, có độ dài cạnh đáy là 3cm và chiều cao là \(2,5\)cm.

Bảo tàng Louvre (Pháp) có một kim tự tháp hình chóp tứ giác đều bằng kính (gọi là kim tự tháp Louvre) có chiều cao \(21,3\)m và cạnh đáy \(34\)m. Tính thể tích của kim tự tháp này.

Hình chóp tứ giác đều có diện tích đáy là \(30{m^2}\), chiều cao \(100\)dm, có thể tích là:
A. \(100{m^3}\) B. \(300{m^3}\) C. \(1000{m^3}\) D. \(300d{m^3}\)
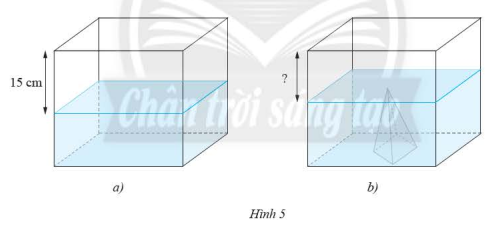
Một bể kính hình hộp chữ nhật chứa nước có hai cạnh đáy là \(50\)cm và \(40\)cm, khoảng cách từ mực nước tới miệng bể là \(15\)cm. Người ta dự định đặt vào bể một khối đá hình chóp tứ giác đều cạnh đáy là \(20\)cm, chiều cao \(15\)cm. Khi đó khoảng cách mực nước tới miệng bể là bao nhiêu? Biết rằng bề dày của đáy bể và thành bể không đáng kể, sau khi đặt khối đá vào, nước ngập khối đá và không tràn ra ngoài.
Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng 15 cm và chiều cao là 8 cm. Tính thể tích của hình chóp tứ giác đều đó.
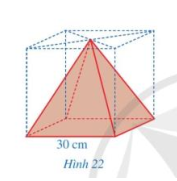
Hình 22 mô tả một vật thể có dạng hình chóp tứ giác đều được tạo ra sau khi cắt bỏ một phần từ một khúc gỗ có dạng hình lập phương với cạnh là 30 cm. Tính thể tích của phần khúc gỗ đã bị cắt bỏ.
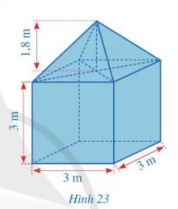
Hình 23 mô tả một lều trại gồm hai phần: phần dưới có dạng hình lập phương với cạnh là 3 m; phần trên có dạng hình chóp tứ giác đều với chiều cao là 1, 8m. Tính thể tích của lều trại đó.
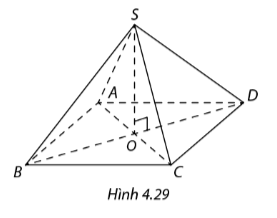
Tính thể tích hình chóp tứ giác đều trong Hình 4.29, biết \(So = 6cm,AB = 5cm.\)
Tính độ dài cạnh đáy của một hình chóp tứ giác đều, biết thể tích của hình chóp bằng \(13,5c{m^3}\) và chiều cao của hình chóp bằng \(4,5cm.\)
Kim tự tháp Cheops ở Ai Cập được xây dựng vào khoảng 2 500 năm trước công nguyên.
a) Kim tự tháp này có dạng hình chóp tứ giác đều với chiều cao \(147m,\) cạnh đáy dài \(230m.\) hãy tính thể tích của nó.
b) Hiện nay, kim tự tháp này vẫn có dạng hình chóp tứ giác đều với chiều cao khoảng \(138m,\) còn độ dài cạnh đáy vẫn khoảng \(230m.\) Thể tích của kim tự tháp giảm bao nhiêu mét khối so với khi mới xây dựng?

Khu bảo tồn Muttart là một phần biểu tượng của cảnh quan thành phố Edmonton, Canada với bốn nhà kính hình dạng kim tự tháp. Mỗi tòa nhà đều từng có chủ đề riêng. Hai nhà kính lớn đều có dạng hình chóp tứ giác đều với chiều cao \(24m\) và diện tích đáy mỗi nhà khoảng \(660{m^2}\). Tính tổng thể tích của hai nhà kính này.
Thả một cái chặn giấy không thấm nước hình chóp tứ giác đều như hình 4.32 vào một chiếc bình đang chứa \(750\,ml\) nước. Hỏi nước có tràn ra khỏi bình không, biết rằng cái chặn giấy chìm hẳn xuống nước và dung tích của bình là \(1\,000\,ml?\)

Một khối bê tông có dạng như hình 4.33. Phần dưới của khối bê tông có dạng hình hộp chữ nhật, đáy là hình vuông cạnh \(30\,cm\) và chiều cao \(25\,cm.\) Phần trên của khối bê tông có dạng hình chóp tứ giác đều, chiều cao \(60cm.\) Tính thể tích của khối bê tông.

Kim tự tháp tại bảo tàng Louvre (Pháp) có dạng hình chóp tứ giác đều với chiều cao \(21,6m\) và cạnh đáy dài \(34m\) (Hình 4.35). Hỏi thể tích của kim tự tháp bằng bao nhiêu mét khối?

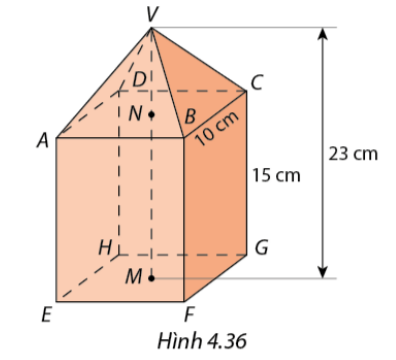
Hình 4.36 là mô hình của một tòa nhà có kết cấu gồm một hình chóp tứ giác đều và một hình hộp chữ nhật. Tính thể tích của mô hình đó.
Từ một khối gỗ hình hộp chữ nhật \(ABCD.EFGH\), người ta cắt ra một hình chóp tứ giác đều \(S.ABCD\) (Hình 4.37). Tính thể tích của khối gỗ còn lại.

Tính thể tích của hình chóp tứ giác đều có chiều cao 24cm, tứ giác đáy có cạnh 15cm.
Một khối gỗ gồm một hình chóp tứ giác đều và một hình lập phương có chung đáy (Hình 3). Tính thể tích của khối gỗ, biết chiều cao của hình chóp tứ giác đều là 50cm và cạnh của hình lập phương là 40cm. (Làm tròn kết quả đến hàng phần mười.)

Cho hình chóp tứ giác đều có cạnh đáy bằng 5m và chiều cao bằng 8m. Thể tích của hình chóp này là
A. \(\frac{{200}}{3}{m^3}\)
B. \(64{m^3}\)
C. \(80{m^3}\)
D. \(\frac{{320}}{3}{m^3}\)
Một chiếc gàu có dạng hình chóp tứ giác đều và một chiếc bình có dạng hình lăng trụ đứng tứ giác có cùng diện tích đáy. Người ta múc đầy 10 gàu nước và đổ vào bình. Hỏi mực nước trong bình tăng thêm bao nhiêu? Cho biết chiều cao của chiếc gàu là 0,3m.
Kim tự tháp Kheops ở Ai Cập được xây dựng vào khoảng 2 500 năm trước Công nguyên. Kim tự tháp này có dạng hình chóp tứ giác đều với độ dài cạnh đáy khoảng 231 m và chiều cao khoảng 146,5 m. Tính thể tích của kim tự tháp đó.
Cho hình chóp tứ giác đều có thể tích bằng \(1,4{m^3}\) và chiều cao bằng 42 dm. Tính độ dài cạnh đáy của hình chóp tứ giác đều đó.
Cho hình chóp tứ giác đều có thể tích bằng \(0,675{m^3}\) và độ dài cạnh đáy bằng 1,5 m. Tính chiều cao của hình chóp tứ giác đều đó.
Cho hai hình chóp tứ giác đều \(S.ABCD\) và \(S.A'B'C'D'\) lần lượt có chiều cao \(SO\) và \(SO'\). Biết \(AB = 2a,A'B' = 3a,SO = 2b,SO' = 3b\) (Hình 12). Tính tỉ số thể tích của hình chóp tứ giác đều \(S.ABCD\) và \(S.A'B'C'D'\) biết rẳng \(a\) và \(b\) cùng đơn vị đo.

Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng \(a\left( {cm} \right)\) và chiều cao bằng \(3a\left( {cm} \right)\). Thể tích của hình chóp đó là:
A. \(3{a^3}\left( {c{m^2}} \right)\)
B. \({a^3}\left( {c{m^2}} \right)\)
C. \(3{a^3}\left( {d{m^2}} \right)\)
D. \({a^3}\left( {c{m^2}} \right)\).
Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng chiều cao. Chứng minh thể tích của hình chóp tứ giác đều đó bằng một phần ba thể tích của hình lập phương có độ dài cạnh bằng độ dài cạnh đáy của hình chóp tứ giác đều đó.
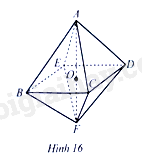
Cho hai hình chóp đều \(A.BCDE\) và \(F.BCDE\) lần lượt có chiều cao là \(AO\) và \(FO\) (Hình 16). Tính tỉ số thể tích của hình chóp tứ giác đều \(A.BCDE\) và \(F.BCDE\) biết \(FO = k.AO\left( {k > 0} \right)\).
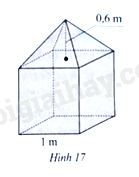
Hình 17 mô tả một khối bê tông mác 200 dùng trong việc xây cầu. Khối bê tông đó gồm hai phần: phần dưới có dạng hình lập phương với độ dài cạnh bằng 1 m, phần trên có dạng hình chóp tứ giác đều với chiều cao bằng 0,6 m. Cần phải chuẩn bị bao nhiêu tấn xi măng và bao nhiêu mét khối nước để làm khối bê tông đó? Biết rằng 1 m3 bê tông mác 200 cần khoảng 350,55 kg xi măng và 185 lít nước.







Danh sách bình luận