Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 4cm và chiều cao bằng 5cm.  Tính độ dài trung đoạn của hình chóp đó.

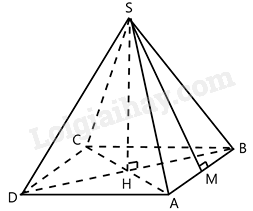
Gọi H là giao hai đường chéo của hình vuông ABCD , M là trung điểm AB.

Vì S.ABCD là hình chóp tứ giác đều nên các mặt bên là tam giác cân => tam giác SAB cân tại S => SM vừa là trung tuyến vừa là đường cao.

Xét tam giác vuông ABC có: \(AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{4^2} + {4^2}}  = 4\sqrt 2  \Rightarrow AH = \frac{1}{2}.AC = 2\sqrt 2 cm\)

SH là chiều cao của hình chóp \( \Rightarrow SH = 5cm\)

Xét tam giác vuông SHA có: \(SA = \sqrt {S{H^2} + A{H^2}}  = \sqrt {{5^2} + {{(2\sqrt 2 )}^2}}  = \sqrt {33} cm\)

Xét tam giác vuông SAM có: \(SM = \sqrt {S{A^2} - A{M^2}}  = \sqrt {{{(\sqrt {33} )}^2} - {{(2)}^2}}  = \sqrt {29} cm\)