Đề bài
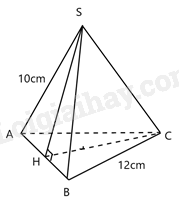
Tính diện tích xung quanh của hình chóp dưới đây.
-
A.
\(108c{m^2}\).
-
B.
\(216c{m^2}\).
-
C.
\(72c{m^2}\).
-
D.
\(144c{m^2}\).
Phương pháp giải
Sử dụng kiến thức về hình chóp đều, định lý Pythagore và công thức tính diện tích xung quanh của hình chóp đều.
Lời giải của GV Loigiaihay.com
Vì S.ABC là hình chóp tam giác đều nên mặt bên SAB là tam giác cân tại S => SH là đường cao đồng thời là trung tuyến của tam giác SAB \( \Rightarrow AH = HB = \frac{{AB}}{2} = \frac{{12}}{2} = 6cm\)
Xét tam giác vuông SHA có: \(SH = \sqrt {S{A^2} - H{A^2}} = \sqrt {{{10}^2} - {6^2}} = 8cm\)
Nửa chu vi đáy của hình chóp: \(p = \frac{{12 + 12 + 12}}{2} = 18cm\)
Vậy diện tích xung quanh của hình chóp S.ABC là \({S_{xq}} = p.d = 18.6 = 108c{m^2}\)
Đáp án : A
