Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H thứ tự là giao điểm của AE, AF với đường chéo DB. Tứ giác AGCH là hình gì?
-
A.
Hình thoi.
-
B.
Hình chữ nhật.
-
C.
Hình bình hành.
-
D.
Hình thang.
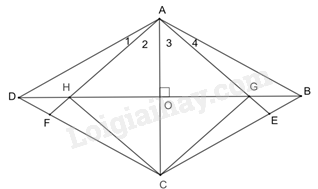
Gọi O là giao điểm của AC và BD thì \(AC \bot BD\) (do O là giao điểm của hai đường chéo của hình thoi)
Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD, ta được:
\(AB = AD;\widehat B = \widehat D;BE = DF\)
Từ đó suy ra \(\Delta ABE = \Delta ADF\)(c-g-c).
Suy ra \(\widehat {A{}_1} = \widehat {{A_4}}\)( hai góc tương ứng).
Mà AC là phân giác của \(\widehat {BAD} \Rightarrow \widehat {{A_2}} = \widehat {{A_3}}\)(1)
Xét tam giác AGH có AO là đường cao, đồng thời là đường phân giác nên tam giác AGH cân tại A.
Suy ra HO = OG (2)
Do ABCD là hình thoi nên AO = OC (tính chất đường chéo của hình thoi) (3)
Từ (1), (2), (3) suy ra: AHCG là hình thoi.
Đáp án : A
Các bài tập cùng chuyên đề
Hãy chọn câu sai.
Điền từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo … là hình thoi”.
Hình thoi không có tính chất nào dưới đây?
Trong các hình sau, hình nào vừa có tâm đối xứng, vừa có trục đối xứng?
Cho các hình sau, chọn khẳng định đúng
Chọn câu trả lời sai.
Hình thoi có chu vi là 32 cm, cạnh hình thoi có độ dài là
Tứ giác dưới đây là hình thoi theo dấu hiệu nào?
Hình thoi có độ dài hai đường chéo là 24cm và 10cm thì cạnh của hình thoi đó bằng
Cho hình thoi ABCD có chu vi bằng 16 cm, đường cao bằng 2 cm. Tính các góc của hình thoi. Hãy chọn câu trả lời đúng.
Tứ giác ABCD có AB = CD. Gọi M, N theo thứ tự là trung điểm của BC, DA. Gọi I, K theo thứ tự là trung điểm của AC và BD và\(MK = \frac{1}{2}CD;IM = \frac{1}{2}AB;NI = \frac{1}{2}CD;KN = \frac{1}{2}AB\). Tứ giác KMIN là hình gì?
Các phương án sau, phương án nào sai?
Hai đường chéo của hình thoi có độ dài lần lượt là 8cm và 10cm. Diện tích của hình thoi đó là ?
Một hình thoi có diện tích là \(\frac{5}{3}d{m^2}\). Biết độ dài một đường chéo bằng \(\frac{{25}}{2}dm\). Tính độ dài đường chéo còn lại.
Cho hình thoi ABCD có O là giao điểm hai đường chéo, biết AC = 16cm và OB = 6cm. Tính CD?
Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB và MD // AC, \({M'}\) là điểm đối xứng với M qua D. Tứ giác \(AMBM'\) là hình gì?
Cho hình thang cân MNPQ. Gọi A, B, C, D lần lượt là các điểm thuộc các cạnh MN, NP, PQ, QM và \(AD = \frac{1}{2}QN\); \(BC = \frac{1}{2}QN,AB = \frac{1}{2}MP,DC = \frac{1}{2}MP\). Tứ giác ABCD là hình gì?
Cho hình thoi ABCD có chu vi bằng 24cm, đường cao bằng 3cm. Tính \(\widehat {DCA}\).
Cho hình thoi ABCD có \(\widehat A\) tù. Biết đường cao kẻ từ đỉnh A đến cạnh CD chia cạnh đó thành hai đoạn bằng nhau. Tính các góc của hình thoi.
Cho hình bình hành ABCD có I là giao điểm hai đường chéo. Biết rằng AC = 6cm và BD = 8cm và AD = 5cm. Tìm khẳng định sai ?
