Đề bài
Cho hình thang cân MNPQ. Gọi A, B, C, D lần lượt là các điểm thuộc các cạnh MN, NP, PQ, QM và \(AD = \frac{1}{2}QN\); \(BC = \frac{1}{2}QN,AB = \frac{1}{2}MP,DC = \frac{1}{2}MP\). Tứ giác ABCD là hình gì?
-
A.
Hình chữ nhật.
-
B.
Hình bình hành.
-
C.
Hình thang cân.
-
D.
Hình thoi.
Phương pháp giải
Chứng minh tứ giác ABCD có bốn cạnh bằng nhau nên ABCD là hình thoi.
Lời giải của GV Loigiaihay.com
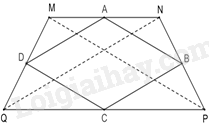
Do MNPQ là hình thang cân nên MP = NQ. (hình thang cân có hai đường chéo bằng nhau). (1)
Xét các tam giác MNQ ; PQN, MNP, QMP ta có:
\(AD = \frac{1}{2}QN\); \(BC = \frac{1}{2}QN,AB = \frac{1}{2}MP,DC = \frac{1}{2}MP\)
Suy ra AB = BC = CD = DA.
Do đó ABCD là hình thoi. (Tứ giác có bốn cạnh bằng nhau là hình thoi.)
Đáp án : D
