Đề bài
Tứ giác ABCD có AB = CD. Gọi M, N theo thứ tự là trung điểm của BC, DA. Gọi I, K theo thứ tự là trung điểm của AC và BD và\(MK = \frac{1}{2}CD;IM = \frac{1}{2}AB;NI = \frac{1}{2}CD;KN = \frac{1}{2}AB\). Tứ giác KMIN là hình gì?
-
A.
Hình chữ nhật.
-
B.
Hình bình hành.
-
C.
Hình thang cân.
-
D.
Hình thoi.
Phương pháp giải
Dựa vào đường trung bình của tam giác chứng minh tứ giác KMIN có
MK = KN = NI = IM suy ra tứ giác KMIN là hình thoi.
Lời giải của GV Loigiaihay.com
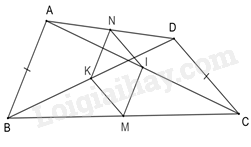
Xét các tam giác BCD, CAB, ADC, DBA ta có:
\(MK = \frac{1}{2}CD;IM = \frac{1}{2}AB;NI = \frac{1}{2}CD;KN = \frac{1}{2}AB\)
Mà AB = CD (giả thiết) .
Suy ra MK = KN = NI = IM.
Tứ giác KMIN có bốn cạnh bằng nhau nên là hình thoi.
Đáp án : D
