: Cho hai hàm số \(y = x + 3\), \(y = mx + 3\left( {m \ne 0} \right)\) có đồ thị lần lượt là các đường thẳng \({d_1}\) và \({d_2}\). Biết rằng đường thẳng \({d_2}\) có cùng hệ số góc với đường thẳng \(y = - x + 5.\) Gọi A là giao điểm của hai đường thẳng \({d_1}\) và \({d_2}\), B là giao điểm của đường thẳng \({d_1}\) với trục Ox, C là giao điểm của đường thẳng \({d_2}\) với trục Ox. Chu vi của tam giác ABC là:
-
A.
\(2\sqrt {18} - 3\)
-
B.
\(2\sqrt {18} + 3\)
-
C.
\(2\sqrt {18} + 6\)
-
D.
\(2\sqrt {18} - 6\)
+ Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
+ Đồ thị hàm số bậc nhất
Ta có: \({d_2}:y = - x + 3\)
Vẽ đồ thị của hai hàm số: \(y = x + 3\) và \(y = - x + 3\):
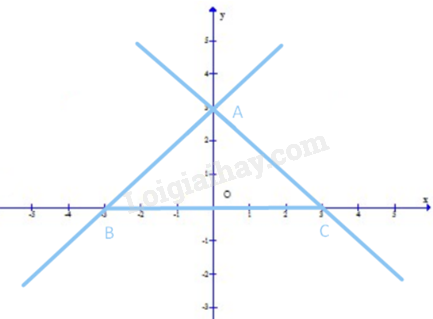
Từ đồ thị ta có, A(3; 0), B(-3; 0), C(3; 0)
Do đó, \(OA = 3,OB = 3,OC = 3,BC = 6\)
Tam giác AOB vuông tại O nên \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{3^2} + {3^2}} = \sqrt {18} \)
Tam giác AOC vuông tại O nên \(AC = \sqrt {O{A^2} + O{C^2}} = \sqrt {{3^2} + {3^2}} = \sqrt {18} \)
Chu vi của tam giác ABC là: \(AB + AC + BC = \sqrt {18} + \sqrt {18} + 6 = 2\sqrt {18} + 6\)
Đáp án : C
Các bài tập cùng chuyên đề
Hệ số góc của đường thẳng \(y = 2x + 1\) là:
Tìm hàm số bậc nhất có hệ số góc bằng 2 và có đồ thị cắt trục tung tại điểm có tung độ bằng \( - 1\).
Cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có hệ số góc là:
Đường thẳng \(y = ax + b\) có hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là:
Chọn khẳng định đúng nhất:
Đường thẳng \(y = \frac{{3x + 1}}{3}\) có hệ số góc là:
Chọn đáp án đúng.
Giá trị của m để đường thẳng \(y = \left( {m + 1} \right)x + 2\left( {m \ne - 1} \right)\) song song với đường thẳng \(y = - 2x + 1\) là:
Tìm các giá trị của m để đường thẳng \(y = \left( {m - 1} \right)x - 2\left( {m \ne 1} \right)\) cắt đường thẳng \(y = 2x\) là:
Hai đường thẳng, \(y = 2mx + 1\left( {m \ne 0} \right)\) và \(y = \left( {m + 1} \right)x + 1\left( {m \ne - 1} \right)\) trùng nhau khi:
Cho các đường thẳng sau: \(y = x + 5;y = - x + 5;y = x + 7;y = - x + 3\)
Có bao nhiêu cặp 2 đường thẳng cắt nhau.
Cho hai hàm số bậc nhất \(y = 2mx + 1\) và \(y = \left( {m + 1} \right)x + m\), có bao nhiêu giá trị của m để đồ thị của hai hàm số đã cho là hai đường thẳng song song?
Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng \(y = 3x + 1\) và đi qua điểm \(\left( {1;7} \right)\)?
Hệ số góc của đường thẳng d biết d đi qua gốc tọa độ O và điểm M(2; 6) là:
Đường thẳng \(y = 2\left( {m + 1} \right)x + m - 2\left( {m \ne - 1} \right)\) đi qua điểm A(1; 9) có hệ số góc là:
Cho hai đồ thị hàm số bậc nhất là hai đường thẳng d: \(y = \left( {m - 2} \right)x - m\) và \(d':y = - 2x - 2mx + 3.\) Với giá trị nào của m thì d cắt d’
Cho hai đường thẳng d: \(y = \left( {m + 2} \right)x + m\) và d’: \(y = - 2x - 2m + 1\). Với giá trị nào của m thì d trùng với d’?
Cho hàm số bậc nhất \(y = 2ax + a - 1\) có đồ thị hàm số là đường d.
Đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: \(y - 4x + 3 = 0\)
Khi đó, điểm A(x; 6) thuộc đường thẳng d thì giá trị của x là:
Hệ số góc của đường thẳng \(\frac{x}{3} + \frac{y}{2} = 1\) là:
Các điểm A(m; 3) và B(1; m) nằm trên đường thẳng có hệ số góc \(m > 0.\) Tìm m.
Cho hàm số bậc nhất \(y = mx + 3\) có đồ thị là đường thẳng d. Biết rằng đường thẳng d song song với đường thẳng \(y = - x\). Gọi A là giao điểm của đường thẳng d với đồ thị của hàm số \(y = x + 1.\) B là giao điểm của đường thẳng d với trục Ox. Diện tích tam giác OAB là:
