Cho hình thang ABCD có hai đáy AB, CD. Hai đường chéo AC và BD cắt nhau tại O. Biết diện tích tam giác OAD là 11 cm2, diện tích tam giác OAB là 5 cm2. Tính diện tích hình thang ABCD.
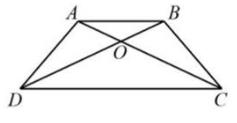
Ta có ${S_{CAB}} = {S_{DAB}}$ (Hai tam giác có chung đáy AB và chiều cao hạ từ D xuống AB bằng chiều cao hạ từ C xuống AB)
Mà ${S_{DAB}} = {S_{OAB}} + {S_{OAD}} = 5 + 11 = 16$ (cm2) nên ${S_{CAB}} = 16c{m^2}$
$ \Rightarrow {S_{OBC}} = {S_{CAB}} - {S_{OAB}} = 16 - 5 = 11$ (cm2)
Xét tam giác AOB và AOD có $\frac{{{S_{AOB}}}}{{{S_{AOD}}}} = \frac{{OB}}{{OD}} = \frac{5}{{11}}$ (chung chiều cao hạ từ A xuống BD nên tỉ số diện tích bằng tỉ số hai đáy)
Xét tam giác OBC và ODC có $\frac{{{S_{OBC}}}}{{{S_{OCD}}}} = \frac{{OB}}{{OD}} \Rightarrow \frac{{11}}{{{S_{ODC}}}} = \frac{5}{{11}}$
Suy ra ${S_{ODC}} = \frac{{11 \times 11}}{{15}} = 24,2$ (cm2)
Vậy ${S_{ABCD}} = {S_{ABD}} + {S_{OBC}} + {S_{ODC}} = 16 + 11 + 24,2 = 51,2$ (cm2)
