Đề bài
(Thi vào 6 trường Hà Nội Amsterdam 2001 – 2002)
Cho tam giác ABC và các điểm D, E, G, H sao cho BD = $\frac{1}{3}$ AB; AE = CG = $\frac{1}{3}$ AC; CH = $\frac{1}{3}$ BC. Tính diện tích hình BDEGH? Biết diện tích của tam giác ABC là 180cm2
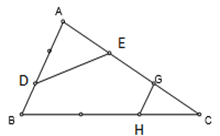
Lời giải của GV Loigiaihay.com
Ta có $\frac{{{S_{ADE}}}}{{{S_{ABC}}}} = \frac{2}{3} \times \frac{1}{3} = \frac{2}{9}$
Suy ra ${S_{ADE}} = \frac{2}{9} \times {S_{ABC}} = \frac{2}{9} \times 180 = 40$ (cm2)
Ta có $\frac{{{S_{CGH}}}}{{{S_{ABC}}}} = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9}$
Suy ra ${S_{CGH}} = \frac{1}{9} \times {S_{ABC}} = \frac{1}{9} \times 180 = 20$ (cm2)
Diện tích hình BDEGH là
180 – (40 + 20) = 120 (cm2)
Đáp số: 120 cm2
