(Đề thi vào lớp 6 môn Toán trường Hà Nội – Amsterdam 2003 – 2004)

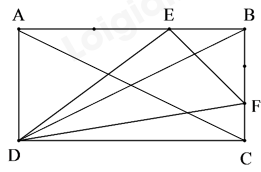
Cho hình chữ nhật ABCD có diện tích 144cm² như hình vẽ. Trên AB lấy điểm E, trên BC lấy điểm F. Các đoạn EB = $\frac{1}{3}$ x AB, CF = $\frac{1}{3}$ x CB. Tính diện tích tam giác DEF.

Nối B với D, A với C

Ta có S_DAB = S_DBC = S_BAC = $\frac{1}{2}$x S_ABCD = $\frac{1}{2}$ x 144 = 72 (cm²)

S_DAE = $\frac{2}{3}$ x S_DAB (Chung chiều cao hạ từ đỉnh D xuống đáy AB và AE = $\frac{2}{3}$ AB)

Suy ra S_DAE = $\frac{2}{3}$ x 72 = 48 (cm²)

S_DFC = $\frac{1}{3}$ x S_DBC (Chung chiều cao hạ từ đỉnh D xuống đáy BC và CF = $\frac{1}{3}$ CB)

Suy ra S_DFC = $\frac{1}{3}$ x 72 = 24 (cm²)

Ta có $\frac{{{S_{BEF}}}}{{{S_{BAC}}}} = \frac{1}{3} \times \frac{2}{3} = \frac{2}{9}$

Suy ra S_BEF = $\frac{2}{9}$ x S_BAC = $\frac{2}{9}$ x 72 = 16 (cm²)

Diện tích tam giác DEF là 144 – (48 + 24 + 16) = 56 (cm²)

                                                       Đáp số: 56 cm²