Cho hình vẽ sau:
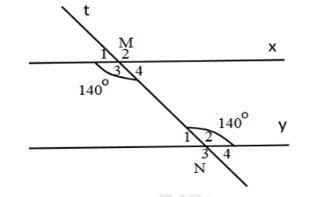
Biết \(\widehat {{M_3}} = \widehat {{N_2}} = {140^0}.\) Tính \(\widehat {{M_4}} + \widehat {{N_2}},\,\widehat {{M_3}} + \widehat {{N_1}}.\)
-
A.
\({115^0}\), \({115^0}\)
-
B.
\({55^0}\), \({55^0}\)
-
C.
\({180^0}\), \({180^0}\)
-
D.
\({145^0}\), \({145^0}\)
Áp dụng tính chất: Tổng hai góc kề bù bằng \({180^0}\).
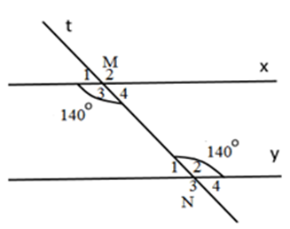
Ta có: \(\widehat {{M_3}} + \widehat {{M_4}} = {180^0}\) (kề bù)
Suy ra \(\widehat {{M_4}} = {180^0} - \widehat {{M_3}} = {180^0} - {140^0} = {40^0}\)
Do đó \(\widehat {{M_4}} + \,\widehat {{N_2}} = {40^0} + {140^0} = {180^0}\)
Ta có: \(\widehat {{N_2}} + \widehat {{N_1}} = {180^0}\) (kề bù)
Suy ra \( \widehat {{N_1}} = {180^0} - \widehat {{N_2}} = {180^0} - {140^0} = {40^0}\)
Do đó \(\widehat {{M_3}} + \widehat {{N_1}} = {140^0} + {40^0} = {180^0}\)
Đáp án : C







