Cho \(\Delta ABC\) nhọn, đường cao $AH.$ Lấy điểm $D$ sao cho $AB$ là trung trực của $HD.$ Lấy điểm $E$ sao cho $AC$ là trung trực của $HE.$ Gọi $M$ là giao điểm của $DE$ với $AB,N$ là giao điểm của $DE$ với $AC.$ Chọn câu đúng.
-
A.
\(\Delta ADE\) là tam giác cân
-
B.
$HA$ là tia phân giác của \(\widehat {MHN}\).
-
C.
A, B đều đúng
-
D.
A, B đều sai
Áp dụng tính chất đường trung trực của đoạn thẳng và tính chất hai tam giác bằng nhau..
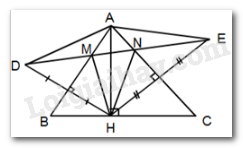
Vì $AB$ là đường trung trực của $HD$ (gt) \( \Rightarrow AD = AH\) (tính chất trung trực của đoạn thẳng)
Vì $AC$ là đường trung trực của $HE$ (gt) \( \Rightarrow AH = AE\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow AD = AE \Rightarrow \Delta ADE\) cân tại $A.$ Nên A đúng.
+) $M$ nằm trên đường trung trực của $HD$ nên $MD = MH$ (tính chất đường trung trực của đoạn thẳng)
Xét \(\Delta AMD\) và \(\Delta AMH\) có:
\(\)$AM$ chung.
$AD = AH$ (cmt)
$MD = MH$ (cmt)
\( \Rightarrow \Delta AMD = \Delta AMH\left( {c - c - c} \right) \Rightarrow \widehat {MDA} = \widehat {MHA}\) (2 góc tương ứng)
Lại có, $N$ thuộc đường trung trực của $HE$ nên $NH = NE$ (tính chất đường trung trực của đoạn thẳng).
+) Xét \(\Delta AHN\) và \(\Delta AEN\) có:
$AN$ chung
$AH = AE$ (cmt)
$NH = NE$ (cmt)
\( \Rightarrow \Delta AHN = \Delta AEN\left( {c - c - c} \right)\)
\(\Rightarrow \widehat {NHA} = \widehat {NEA}\) (2 góc tương ứng)
Mà \(\Delta ADE\) cân tại $A$ (cmt) \( \Rightarrow \widehat {MDA} = \widehat {NEA} \Rightarrow \widehat {MHA} = \widehat {NHA}\) .
Vậy $HA$ là đường phân giác của \(\widehat {MHN}\) .
Đáp án : C








Danh sách bình luận