Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
-
A.
Tam giác vuông
-
B.
Tam giác cân
-
C.
Tam giác đều
-
D.
Tam giác vuông cân
Áp dụng tính chất đường trung trực và đường trung tuyến của tam giác.
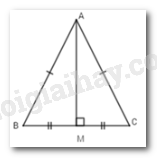
Giả sử \(\Delta ABC\) có $AM$ là trung tuyến đồng thời là đường trung trực.
Ta sẽ chứng minh \(\Delta ABC\) là tam giác cân.
Thật vậy, vì $AM$ là trung tuyến của \(\Delta ABC\) (gt) \( \Rightarrow BM = MC\) (tính chất trung tuyến)
Vì $AM$ là trung trực của $BC$ $ \Rightarrow AM \bot BC$
Xét hai tam giác vuông \({\Delta}ABM\) và \({\Delta}ACM\) có:
\(BM = CM\left( {cmt} \right)\)
$AM$ chung
\( \Rightarrow \Delta ABM = \Delta ACM\) (2 cạnh góc vuông)
\( \Rightarrow AB = AC\) (2 cạnh tương ứng) \( \Rightarrow \Delta ABC\) cân tại $A.$
Đáp án : B
Các bài tập cùng chuyên đề
Gọi $O$ là giao điểm của ba đường trung trực trong \(\Delta ABC\). Khi đó $O$ là:
Cho \(\Delta ABC\) cân tại $A,$ có \(\widehat A = {40^0}\), đường trung trực của $AB$ cắt $BC$ ở $D.$ Tính \(\widehat {CAD}\).
Cho tam giác \(ABC\) trong đó \(\widehat A = 100^\circ \). Các đường trung trực của \(AB\) và \(AC\) cắt cạnh \(BC\) theo thứ tự ở \(E\) và \(F\) . Tính \(\widehat {EAF}.\)
Cho \(\Delta ABC\) nhọn, đường cao $AH.$ Lấy điểm $D$ sao cho $AB$ là trung trực của $HD.$ Lấy điểm $E$ sao cho $AC$ là trung trực của $HE.$ Gọi $M$ là giao điểm của $DE$ với $AB,N$ là giao điểm của $DE$ với $AC.$ Chọn câu đúng.
Cho \(\Delta ABC\) vuông tại $A,$ có \(\widehat C = {30^0}\), đường trung trực của $BC$ cắt $AC$ tại $M.$ Em hãy chọn câu đúng:
Cho tam giác $ABC$ vuông tại $A,$ kẻ đường cao $AH.$ Trên cạnh $AC$ lấy điểm $K$ sao cho $AK = AH.$ Kẻ \(KD \bot AC\left( {D \in BC} \right)\). Chọn câu đúng.
Cho tam giác \(ABC\) cân tại \(A\) có \(AM\) là đường trung tuyến khi đó
Cho \(\Delta ABC\) cân tại $A,$ hai đường cao $BD$ và $CE$ cắt nhau tại $I.$ Tia $AI$ cắt $BC$ tại $M.$ Khi đó \(\Delta MED\) là tam giác gì?
Cho tam giác \(ABC\) nhọn có trực tâm \(H.\) Chọn câu đúng.
Cho đoạn thẳng $AB$ và điểm $M$ nằm giữa $A$ và $B$$\;\left( {MA < MB} \right).$ Vẽ tia $Mx$ vuông góc với $AB,$ trên đó lấy hai điểm $C$ và $D$ sao cho $MA = MC,MD = MB.$ Tia $AC$ cắt $BD$ ở $E.$ Tính số đo \(\widehat {AEB}\)
