Cho tam giác \(ABC\) có: \(\widehat B = 2\widehat C,\) các đường phân giác của góc \(B\) và \(C\) cắt nhau tại \(I.\) Chọn câu đúng.
-
A.
\(AC = AB + IB\)
-
B.
\(AC = AB + IA\)
-
C.
\(AC = AB + IC\)
-
D.
\(AC = BC + IB\)
+ Kẻ \(ID \bot BC;IE \bot AC;IF \bot AB\)
+ Sử dụng tính chất ba đường phân giác của tam giác, chứng minh \(AI\) là phân giác của \(\widehat {BAC}\)
+ Chứng minh \(BF = BD;\) \(AF = AE;CE = CD\)
+ Trên đoạn \(DC\) lấy điểm \(G\) sao cho \(BD = DG\), chứng minh \(IB = IG\)
+ Chứng minh \(IG//AC\)
+ Chứng minh \(IG = GC\)
+ Từ các điều trên ta tính được \(AC\).
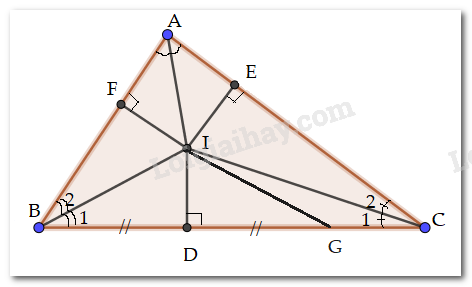
Kẻ \(ID \bot BC;IE \bot AC;IF \bot AB\)
Tam giác \(ABC\) có các đường phân giác của góc \(\widehat {ABC}\) và \(\widehat {ACB}\) cắt nhau tại \(I\) nên \(AI\) là phân giác của \(\widehat {BAC}\) (tính chất ba đường phân giác của tam giác)
Vì \(BI\) là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{{\widehat {ABC}}}{2}\) (tính chất tia phân giác)
Xét \(\Delta BFI\) vuông tại \(F\) và \(\Delta BDI\) vuông tại \(D\) có:
\(\widehat {{B_1}} = \widehat {{B_2}}\) (cmt)
\(BI\) là cạnh chung
Do đó \(\Delta BFI = \Delta BDI\) (cạnh huyền – góc nhọn) \( \Rightarrow BF = BD\) (hai cạnh tương ứng)
Chứng minh tương tự ta có: \(AF = AE;CE = CD\).
Trên đoạn \(DC\) lấy điểm \(G\) sao cho \(BD = DG\).
Xét \(\Delta BDI\) vuông tại \(D\) và \(\Delta GDI\) vuông tại \(D\) có:
\(BD = DG\) (theo cách vẽ)
\(DI\) là cạnh chung
Do đó \(\Delta BDI = \Delta GDI\) (hai cạnh góc vuông) \( \Rightarrow IB = IG\) (hai cạnh tương ứng) \( \Rightarrow \Delta IBG\) là tam giác cân tại \(I\)
\( \Rightarrow \widehat {{B_1}} = \widehat {IGB}\) (tính chất tam giác cân) \((1)\)
Ta có: \(\widehat {ABC} = 2\widehat {ACB} \Rightarrow \widehat {ACB} = \dfrac{{\widehat {ABC}}}{2} = \widehat {{B_1}}\) \((2)\)
Từ \((1)\); \((2)\) suy ra: \( \Rightarrow \widehat {IGB} = \widehat {ACB}\) mà hai góc này ở vị trí đồng vị nên \(IG//AC\) (dấu hiệu nhận biết hai đường thẳng song song)
Khi đó \(\widehat {{C_2}} = \widehat {GIC}\) (hai góc so le trong)
Mặt khác: \(\widehat {{C_2}} = \widehat {{C_1}}\) (do \(CI\) là tia phân giác của \(\widehat {ACB}\))
\( \Rightarrow \widehat {{C_1}} = \widehat {GIC} \Rightarrow \Delta GIC\) cân tại \(G\) \( \Rightarrow IG = GC\) (định nghĩa tam giác cân)
Ta có: \(AC = AE + CE\)
\(\begin{array}{l} = AF + CD\\ = AF + DG + GC\\ = AF + BD + IG\\ = AF + BF + IB\\ = AB + IB\end{array}\)
Đáp án : A








Danh sách bình luận