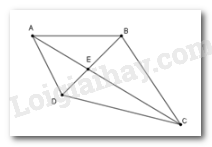
Cho hình vẽ dưới đây. Chọn câu đúng.
-
A.
$AB + BC + CD + DA < AC + BD$
-
B.
$AB + BC + CD + DA < 2\left( {AC + BD} \right)$
-
C.
$AB + BC + CD + DA > 2\left( {AC + BD} \right)$
-
D.
$AB + BC + CD + DA = 2\left( {AC + BD} \right)$
Sử dụng quan hệ giữa ba cạnh của một tam giác: Trong một tam giác, độ dài của một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh kia.
Áp dụng quan hệ giữa ba cạnh của một tam giác:
Xét tam giác \(AED\) có \(AE + ED > AD\,\,\,\left( 1 \right)\)
Xét tam giác \(ECD\) có \(CE + DE > CD\,\,\left( 2 \right)\)
Xét tam giác \(EBC\) có \(EB + EC > BC\,\left( 3 \right)\)
Xét tam giác \(ABE\) có \(AE + EB > AB\,\,\,\left( 4 \right)\)
Từ \(\left( 1 \right);\left( 2 \right);\left( 3 \right);\left( 4 \right)\) ta có \(AE + DE + CE + DE + BE + CE + AE + BE > AD + CD + BC + AB\)
Mà \(AE + EC = AC;\,DE + BE = BD\) nên \(2\left( {AC + BD} \right) > AB + BC + CD + DA\) .
Đáp án : B
Các bài tập cùng chuyên đề
Cho \(\Delta ABC\), em hãy chọn đáp án sai trong các đáp án sau:
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
Cho \(\Delta ABC\) có cạnh $AB = 2cm$ và cạnh \(BC = 6cm\). Tính độ dài cạnh $AC$ biết độ dài cạnh $AC$ là một số tự nhiên chẵn.
Cho tam giác \(ABC\) biết \(AB = 1\,cm;\,BC = 6\,cm\) và cạnh \(AC\) là một số nguyên. Chu vi tam giác \(ABC\) là
Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng $5cm.$ Tính cạnh $BC$ của tam giác đó biết chu vi của tam giác là $17cm.$
Cho \(\Delta ABC\) có $M$ là trung điểm $BC.$ So sánh $AB + AC$ và $2AM.$
Cho \(\Delta ABC\) có điểm $O$ là một điểm bất kì nằm trong tam giác. So sánh \(OA + OC\) và \(AB + BC\).
Cho \(\Delta ABC\) có \(D\) là trung điểm của \(BC\). Trong các khẳng định sau khẳng định nào đúng?
