Cho \(\Delta ABC\) có điểm $O$ là một điểm bất kì nằm trong tam giác. So sánh \(OA + OC\) và \(AB + BC\).
-
A.
\(OA + OC < BA + BC\)
-
B.
\(OA + OC > BA + BC\)
-
C.
\(OA + OC = BA + BC\)
-
D.
\(OA + OC \ge BA + BC\).
- Gọi giao điểm của $AO$ và $BC$ là $D.$
- Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.
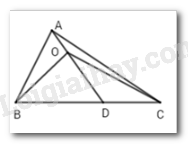
Gọi giao điểm của $AO$ và $BC$ là $D.$ Do $O$ nằm trong \(\Delta ABC\) nên $D$ nằm giữa $B$ và $C$\( \Rightarrow BC = BD + DC\left( * \right)\)
Xét \(\Delta ABD\) có: \(AD < AB + BD\) (bất đẳng thức tam giác)
\( \Rightarrow OA + OD < AB + BD\left( 1 \right)\)
Xét \(\Delta OCD\) có: \(OC < OD + DC\left( 2 \right)\) (bất đẳng thức tam giác)
Cộng vế với vế của \(\left( 1 \right)\) và \(\left( 2 \right)\) ta được:
\(OA + OD + OC < AB + BD + OD + DC\) \( \Rightarrow OA + OC < AB + BD + DC\left( {**} \right)\)
Từ \(\left( * \right)\) và \(\left( {**} \right)\) ta có: \(OA + OC < AB + BC.\)
Đáp án : A
Các bài tập cùng chuyên đề
Cho \(\Delta ABC\), em hãy chọn đáp án sai trong các đáp án sau:
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
Cho \(\Delta ABC\) có cạnh $AB = 2cm$ và cạnh \(BC = 6cm\). Tính độ dài cạnh $AC$ biết độ dài cạnh $AC$ là một số tự nhiên chẵn.
Cho tam giác \(ABC\) biết \(AB = 1\,cm;\,BC = 6\,cm\) và cạnh \(AC\) là một số nguyên. Chu vi tam giác \(ABC\) là
Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng $5cm.$ Tính cạnh $BC$ của tam giác đó biết chu vi của tam giác là $17cm.$
Cho \(\Delta ABC\) có $M$ là trung điểm $BC.$ So sánh $AB + AC$ và $2AM.$
Cho hình vẽ dưới đây. Chọn câu đúng.
Cho \(\Delta ABC\) có \(D\) là trung điểm của \(BC\). Trong các khẳng định sau khẳng định nào đúng?
