Cho góc \(\widehat {xOy} = {60^0},\) \(A\) là điểm trên tia \(Ox,\,B\) là điểm trên tia \(Oy\) \((A,B\) không trùng với \(O).\)
Chọn câu đúng nhất.
-
A.
\(OA + OB \le 2AB\)
-
B.
\(OA + OB = 2AB\) khi \(OA = OB.\)
-
C.
\(OA + OB \ge 2AB\)
-
D.
Cả A, B đều đúng.
Kẻ tia phân giác \(Ot\) của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{{{60}^o}}}{2} = {30^o}.\)
Gọi \(I\) là giao của \(Ot\) và \(AB\). Kẻ \(AH \bot Ot, BK \bot Ot\)
Xét \(\Delta OAH\) có \(\widehat {AOH} = {30^o}\) nên \(OA = 2AH.\) Từ đó so sánh \(OA\) và \(AI\) (1)
Xét \(\Delta OBK\) có \(\widehat {BOK} = {30^o}\) nên \(OB = 2BK.\) Từ đó so sánh \(OB\) và \(BI\) (2)
Từ (1) và (2) ta so sánh được \(OA + OB\) với \(2AB.\) Từ đó xét khi nào dấu “=” xảy ra.
* Chú ý: Trong tam giác vuông, cạnh đối diện với góc \({30^o}\) bằng nửa cạnh huyền.
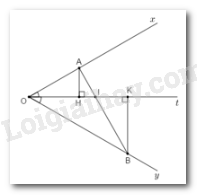
Kẻ tia phân giác \(Ot\) của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{{{60}^o}}}{2} = {30^o}.\)
Gọi \(I\) là giao của \(Ot\) và \(AB\). Kẻ \(AH \bot Ot, BK \bot Ot\)
Xét \(\Delta OAH\) có \(\widehat {AOH} = {30^o}\) nên \(OA = 2AH.\)
Vì \(AH,\,AI\) lần lượt là đường vuông góc, đường xiên kẻ từ \(A\) đến \(Ot\) nên \(AH \le AI\) do đó \(OA \le 2AI\) (1)
Xét \(\Delta OBK\) có \(\widehat {BOK} = {30^o}\) nên \(OB = 2BK.\)
Vì \(BK,\,BI\) lần lượt là đường vuông góc, đường xiên kẻ từ \(B\) đến \(Ot\) nên \(BK \le BI\) do đó \(OB \le 2BI\) (2)
Cộng (1) với (2) theo vế với vế ta được:
\(OA + OB \le 2AI + 2BI = 2\left( {AI + BI} \right) = 2AB\)
Dấu “=” xảy ra khi và chỉ khi \(H,\,I,K\) trùng nhau hay \(AB \bot Ot\) suy ra \(\widehat {AIO} = \widehat {BIO} = {90^o}.\)
Xét \(\Delta OAI\) và \(\Delta OBI\) có:
\(\widehat {AIO} = \widehat {BIO} = {90^o}\)
\(\widehat {AOI} = \widehat {BOI}\) (vì \(Ot\) là phân giác của \(\widehat {xOy}\))
\(OI\) cạnh chung
\( \Rightarrow \Delta OAI = \Delta OBI\) (g.c.g)
\( \Rightarrow OA = OB\) (hai cạnh tương ứng).
Vậy \(OA + OB = 2AB\) khi \(OA = OB.\)
Đáp án : D








Danh sách bình luận