Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Chọn khẳng định đúng nhất
-
A.
Tam giác AMB đều
-
B.
AM = BM = CM
-
C.
AM = BC
-
D.
AB + AC = BC
Sử dụng các trường hợp bằng nhau của tam giác, suy ra các cạnh tương ứng bằng nhau.
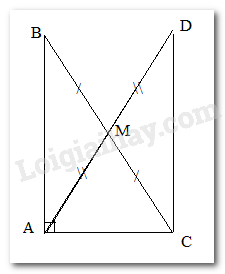
Trên tia đối của tia MA lấy điểm D sao cho MA = MD. Khi đó, 2. AM = AD
Xét tam giác ABM và DCM, có:
AM = DM
\(\widehat {AMB} = \widehat {CMD}\) ( đối đỉnh)
BM = CM ( gt)
\( \Rightarrow \Delta ABM = \Delta DCM\) ( c.g.c)
\( \Rightarrow \widehat {ABC} = \widehat {BCD}\) (2 góc tương ứng); AB = CD ( 2 cạnh tương ứng)
Mà 2 góc ABC và BCD ở vị trí so le trong
\( \Rightarrow \)AB // CD
Mà AB \( \bot \) AC
\( \Rightarrow \) CD \( \bot \) AC ( tính chất)
Xét tam giác vuông ABC và CDA có:
AC chung
\(\widehat {BAC} = \widehat {DCA}( = 90^\circ )\)
AB = CD( cmt)
\( \Rightarrow \Delta ABC = \Delta CDA\) ( c.g.c)
\( \Rightarrow \) AD = BC ( 2 cạnh tương ứng)
\( \Rightarrow \) 2. AM = BC
\( \Rightarrow \) AM = MB = MC
Đáp án : B
