Cho tam giác ABC có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều AMB và ANC.
Khẳng định đúng là:
-
A.
BN = CM
-
B.
BM = CN
-
C.
\(\widehat {MAN} = 120^\circ \)
-
D.
\(\Delta MBN = \Delta NCM\)
Để chứng minh ai cạnh bằng nhau ta sử dụng các trường hợp bằng nhau của tam giác để chứng minh hai tam giác bằng nhau từ đó suy ra hai cạnh tương ứng bằng nhau.
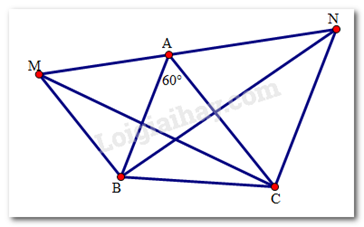
Ta có:
\(\begin{array}{l}\widehat {MAC} = \widehat {MAB} + \widehat {BAC} = {60^0} + {60^0} = {120^0}\\\widehat {BAN} = \widehat {CAN} + \widehat {BAC} = {60^0} + {60^0} = {120^0}\end{array}\)
\( \Rightarrow \)\(\widehat {MAC} = \widehat {BAN}\) .
Xét hai tam giác ABN và AMC có:
AM = AB (do tam giác AMB đều)
\(\widehat {MAC} = \widehat {BAN}\) (cmt)
AN = AC (do tam giác ANC đều)
Do đó \(\Delta ABN = \Delta AMC(c.g.c)\)
\( \Rightarrow \)BN = CM (hai cạnh tương ứng).
Đáp án : A
Các bài tập cùng chuyên đề
Chọn câu sai.
Hai góc nhọn của tam giác vuông cân bằng nhau và bằng
Cho tam giác $ABC$ cân tại $A.$ Phát biểu nào trong các phát biểu sau là sai:
Một tam giác cân có góc ở đỉnh bằng \({64^0}\) thì số đo góc ở đáy là:
Một tam giác cân có góc ở đáy bằng \({70^0}\) thì số đo góc ở đỉnh là:
Số tam giác cân trong hình vẽ dưới đây là:
Tính số đo \(x\) trên hình vẽ sau:
Cho tam giác $ABC$ cân tại đỉnh $A$ với \(\widehat A = {80^0}\). Trên hai cạnh $AB,AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $AD = AE.$ Phát biểu nào sau đây là sai?
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ ;\,AB = AC\). Khi đó
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM = \dfrac{{BC}}{2}\). Số đo góc \(BAC\) là
Tam giác \(ABC\) có \(\widehat A = 40^\circ ;\,\widehat B - \widehat C = 20^\circ .\) Trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AB.\) Tính số đo góc \(CBE.\)
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ .\) Trên tia phân giác của góc \(A\) lấy điểm \(D\) sao cho \(AD = AB + AC.\) Khi đó tam giác \(BCD\) là tam giác gì?
Cho tam giác $ABC$ có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều $AMB$ và $ANC.$
Để hai tam giác cân bằng nhau thì phải cần điều kiện là:
Cho tam giác ABC cân tại A. Phát biểu nào trong các phát biểu sau là sai:
Một tam giác cân có góc ở đỉnh bằng \({54^0}\) thì số đo góc ở đáy là:
Phát biểu nào sau đây là đúng:
Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt BC tại K và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I.
Cho tam giác ABC cân tại đỉnh A với \(\widehat A = {80^0}\). Trên hai cạnh AB, AC lần lượt lấy hai điểm D và E sao cho AD = AE. Phát biểu nào sau đây là sai?
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Chọn khẳng định đúng nhất
